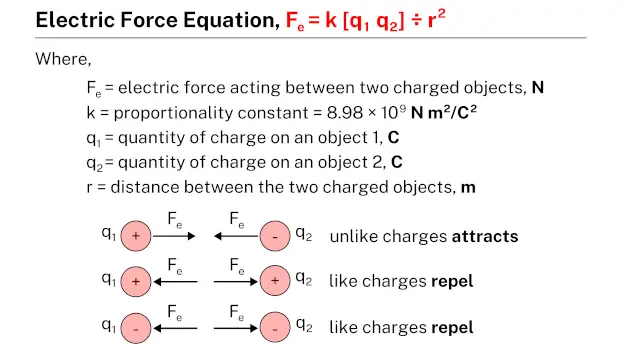
Electric force equation

by

The information on this page is ✔ fact-checked.

Electric force equation
Electric force equation | Image: Learnool

The electric force equation, based on Coulomb’s law, allows us to calculate the force between two charged objects. It is expressed as Fe = k [q1 q2] ÷ r2, where Fe represents the electric force, k is the Coulomb’s constant, q1 and q2 are the charges of the objects, and r is the distance between the two charged objects.

Practice problems

Problem #1

Calculate the electric force acting between two objects, object 1 and object 2, with charges of 20 µC and 15 µC, respectively, separated by a distance of 1 m. Take the value of the proportionality constant, k, as 8.98 × 109 N m2/C2.

Solution

Given data:

  • Electric force acting between two charged objects, Fe = ?
  • Quantity of charge on object 1, q1 = 20 µC = 20 × 10-6 C
  • Quantity of charge on object 2, q2 = 15 µC = 15 × 10-6 C
  • Distance between the two charged objects, r = 1 m
  • Proportionality constant, k = 8.98 × 109 N m2/C2

Applying the formula:

  • Fe = k [q1 q2] ÷ r2
  • Fe = [(8.98 × 109) × (20 × 10-6) × (15 × 10-6)] ÷ (1)2
  • Fe = [8.98 × 20 × 15 × 10-3] ÷ 1
  • Fe = 8.98 × 20 × 15 × 10-3
  • Fe = 2.69 N

Therefore, the electric force acting between two charged objects is 2.69 N.

Problem #2

Determine the electric force acting between two charged plastic balls separated by a distance of 150 cm. The proportionality constant, k, is 8.98 × 109 N m2/C2. The charges of the balls are q1 = 16 µC and q2 = 8 µC.

Solution

Given data:

  • Electric force acting between two charged plastic balls, Fe = ?
  • Distance between the two charged plastic balls, r = 150 cm = 1.5 m
  • Proportionality constant, k = 8.98 × 109 N m2/C2
  • Quantity of charge on 1st plastic ball, q1 = 16 µC = 16 × 10-6 C
  • Quantity of charge on 2nd plastic ball, q2 = 8 µC = 8 × 10-6 C

Applying the formula:

  • Fe = k [q1 q2] ÷ r2
  • Fe = [(8.98 × 109) × (16 × 10-6) × (8 × 10-6)] ÷ (1.5)2
  • Fe = [8.98 × 16 × 8 × 10-3] ÷ 2.25
  • Fe = 1.1494 ÷ 2.25
  • Fe = 0.51 N

Therefore, the electric force acting between two charged plastic balls is 0.51 N.

Problem #3

Given two spheres with charges of 30 µC and 7 µC, placed 2.1 m apart, find the value of the electric force acting between them. The proportionality constant, k, is 8.98 × 109 N m2/C2.

Solution

Given data:

  • Quantity of charge on sphere 1, q1 = 30 µC = 30 × 10-6 C
  • Quantity of charge on sphere 2, q2 = 7 µC = 7 × 10-6 C
  • Distance between the two charged spheres, r = 2.1 m
  • Electric force acting between two charged spheres, Fe = ?
  • Proportionality constant, k = 8.98 × 109 N m2/C2

Applying the formula:

  • Fe = k [q1 q2] ÷ r2
  • Fe = [(8.98 × 109) × (30 × 10-6) × (7 × 10-6)] ÷ (2.1)2
  • Fe = [8.98 × 30 × 7 × 10-3] ÷ 4.41
  • Fe = 1.8858 ÷ 4.41
  • Fe = 0.42 N

Therefore, the electric force acting between two charged spheres is 0.42 N.

Problem #4

Calculate the magnitude of the electric force between two charged balloons, separated by a distance of 250 cm. The proportionality constant, k, is 8.98 × 109 N m2/C2. The charges of the balloons are q1 = -25 µC and q2 = 5 µC.

Solution

Given data:

  • Electric force acting between two charged balloons, Fe = ?
  • Distance between the two charged sphere, r = 250 cm = 2.5 m
  • Proportionality constant, k = 8.98 × 109 N m2/C2
  • Quantity of charge on balloon 1, q1 = -25 µC = -25 × 10-6 C
  • Quantity of charge on balloon 2, q2 = 5 µC = 5 × 10-6 C

Applying the formula:

  • Fe = k [q1 q2] ÷ r2
  • Fe = [(8.98 × 109) × (-25 × 10-6) × (5 × 10-6)] ÷ (2.5)2
  • Fe = [8.98 × (-25) × 5 × 10-3] ÷ 6.25
  • Fe = (-1.1225) ÷ 4.41
  • Fe = -0.25 N
  • |Fe| = |-0.25| = 0.25 N

Therefore, the magnitude of electric force acting between the two charged balloons is 0.25 N.

Related

External links

Deep

Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.

Leave a Comment