Free fall

Updated on by

The information on this page is ✔ fact-checked.

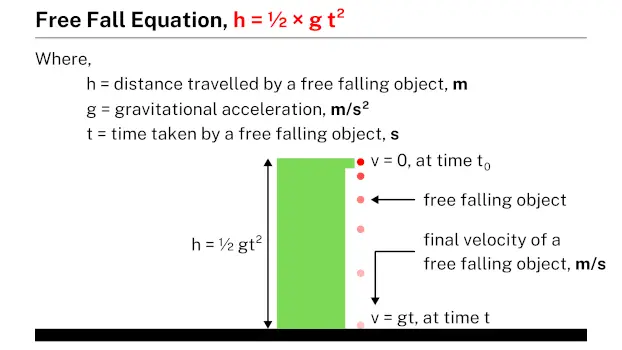
Free fall equation
Free fall equation | Image: Learnool

Free fall is the motion of an object under the influence of gravity alone, without any other forces acting on it, such as air resistance. In a vacuum, where air resistance is negligible, all objects fall at the same rate regardless of their mass. For example, if you drop a feather and a rock from the same height in a vacuum, they will hit the ground simultaneously. On Earth, free fall can be observed when you drop an object from a height and it accelerates downward due to gravity, typically at a rate of 9.8 meters per second squared. Free fall is an important concept in physics as it helps explain the motion of objects under the influence of gravity and is a fundamental aspect of understanding gravitational forces.

Practice problems

Problem #1

A feather is released from the top of a building, free-falling for a time of 20 seconds. Calculate the distance traveled by the feather during this time and determine its velocity. Assume a gravitational acceleration of g = 9.81 m/s2.

Solution

Given data:

  • Time taken by a feather, t = 20 s
  • Distance traveled by a feather, h = ?
  • Velocity of a feather, v = ?
  • Gravitational acceleration, g = 9.81 m/s2

Applying the formula of free fall distance, in terms of time:

  • h = ½ × g t2
  • h = ½ × 9.81 × (20)2
  • h = ½ × 9.81 × 400
  • h = 1962 m

Therefore, the distance traveled by a feather is 1962 m.

Applying the formula of free fall velocity, in terms of time:

  • v = g t
  • v = 9.81 × 20
  • v = 196.2 m/s

Therefore, the velocity of a feather is 196.2 m/s.

Problem #2

A ball is dropped from the top of a tower and falls a distance of 600 meters. Determine the time it takes for the ball to reach the ground and calculate its velocity upon reaching the ground. Use a gravitational acceleration of g = 9.81 m/s2.

Solution

Given data:

  • Distance traveled by a ball, h = 600 m
  • Time taken by a ball to reach the ground, t = ?
  • Velocity of a ball, v = ?
  • Gravitational acceleration, g = 9.81 m/s2

Applying the formula of free fall time, in terms of distance:

  • t = √2 h/g
  • t = √(2 × 600)/9.81
  • t = √1200/9.81
  • t = √122.3241
  • t = 11.06 s

Therefore, the time taken by a ball to reach the ground is 11.06 s.

Applying the formula of free fall velocity, in terms of distance:

  • v = √2 g h
  • v = √2 × 9.81 × 600
  • v = √11772
  • v = 108.49 m/s

Therefore, the velocity of a ball is 108.49 m/s.

Problem #3

A small piece of paper is dropped from the 10th floor of a building and falls with an initial velocity of 26 m/s. Determine the time it takes for the paper to reach the ground and calculate the distance traveled by the paper. Use a gravitational acceleration of g = 9.81 m/s2.

Solution

Given data:

  • Velocity of a paper, v = 26 m/s
  • Time taken by a paper to reach the ground, t = ?
  • Distance traveled by a paper, h = ?
  • Gravitational acceleration, g = 9.81 m/s2

Applying the formula of free fall time, in terms of velocity:

  • t = v/g
  • t = 26/9.81
  • t = 2.65 s

Therefore, the time taken by a piece of paper to reach the ground is 2.65 s.

Applying the formula of free fall distance, in terms of velocity:

  • h = v2/2 g
  • h = (26)2/(2 × 9.81)
  • h = 676/19.62
  • h = 34.45 m

Therefore, the distance traveled by a piece of paper is 34.45 m.

Problem #4

A box is released from a tower and takes 4 seconds to reach the ground. Calculate the distance traveled by the box during its free fall. Assume a gravitational acceleration of g = 9.81 m/s2.

Solution

Given data:

  • Time taken by a box to reach the ground, t = 4 s
  • Distance traveled by a box, h = ?
  • Gravitational acceleration, g = 9.81 m/s2

Applying the formula of free fall distance, in terms of time:

  • h = ½ × g t2
  • h = ½ × (9.81) × (4)2
  • h = ½ × 9.81 × 16
  • h = 78.48 m

Therefore, the distance travelled by a box is 78.48 m.

More topics

External links

Deep

Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.

Leave a Comment