Gravity

Updated on by

The information on this page is ✔ fact-checked.

Gravity is a force that attracts objects towards the center of the Earth or towards any other massive physical body. It is a fundamental force of nature that acts on all objects with mass. Gravity plays a significant role in shaping the structure of the universe and governing the motion of celestial bodies. For example, it keeps planets in their stable orbits around the Sun. The strength of gravity depends on the mass of the objects involved, with larger objects exerting a stronger gravitational pull.

Examples

Water droplet

Gravity example - Water droplet
Gravity pulling a water droplet off a leaf | Image: Pixabay

During the rainy season, water droplets can be observed hanging on the edges of leaves, ready to fall. This phenomenon demonstrates the force of gravity in action. It is the force of gravity that pulls these water droplets downward, directing them towards the ground.

Slipped coin

Gravity example - Slipped coin
Gravity drawing a slipped coin downward | Image: Pixabay

Visualize yourself holding a handful of coins in your hand. As you gradually release your grip, some of the coins slip and fall downward. This simple yet illustrative scenario perfectly captures the force of gravity in action. Gravity, the fundamental force that attracts objects towards the Earth, is the reason behind the coins descending from your hand.

Tennis ball

Gravity example - Tennis ball
Gravity pulling a thrown-up tennis ball back to the ground | Image: Stock photo

Imagine playing with a tennis ball and tossing it into the air. It becomes evident that gravity is at work as the ball is always pulled downward. Regardless of the height to which it is thrown, the ball always descends towards the ground. This behavior of the tennis ball demonstrates the presence of gravity.

Tap water

Gravity example - Tap water
Gravity causing water to fall from a tap | Image: Pixabay

When a tap is opened, water flows out due to the pressure created by the water supply system. As water flows out of the tap, it is pulled downwards towards the ground by gravity, which is the natural force that pulls all objects towards the center of the Earth. Gravity acts on everything, including water, causing it to move downwards in a straight line. So, when water is seen falling from a tap, it’s because gravity is pulling it downwards towards the Earth.

Waterfall

Gravity example - Waterfall
Gravity guiding water as it cascades down a waterfall | Image: Pexels

When observing a waterfall, one can witness the water gracefully descending downwards. This downward motion of the water is attributed to the force of gravity. Irrespective of the quantity of water flowing from the waterfall, it consistently moves downward, driven by the pull of gravity.

Flying kite

Gravity example - Flying kite
Gravity attracting a flying kite towards the Earth | Image: Pixabay

During the festival of Makar Sankranti, which involves flying kites, it is common to witness kites descending gracefully to the ground when they become detached from the thread. This phenomenon serves as a visible demonstration of the force of gravity at work.

Dropped ball

Gravity example - Dropped ball
Gravity accelerating a dropped ball from a height | Image: Learnool

When a ball is released from a certain height, it consistently moves downward towards the ground. This observation highlights the effect of gravity. Regardless of the ball’s weight, whether it is heavy or light, or the height from which it is dropped, it always experiences the downward pull of gravity.

Swimming

Gravity example - Swimming
Gravity attracting a swimmer as they leap into a swimming pool | Image: Pixabay

When swimmers jump into a swimming pool, they experience the force of gravity pulling them downwards. Simultaneously, the upward buoyant force exerted by the water counteracts the force of gravity, resulting in the swimmers being pushed upwards. The interplay between gravity and buoyancy plays a crucial role in determining the behavior of objects submerged in a fluid medium, such as water.

Apple

Gravity example - Apple
Gravity pulling an apple down from a tree | Image: Pixabay

Fruits growing on trees and naturally falling to the ground when ripe is a clear demonstration of gravity in action. The force of gravity, discovered by Sir Isaac Newton, is responsible for pulling the apple and other fruits downwards from the tree and causing them to land on the ground. This fundamental force of nature acts on all objects with mass, like the apple, and attracts them towards the center of the Earth.

Water sprinkler

Gravity example - Water sprinkler
Gravity guiding water released from a water sprinkler | Image: Stock photo

When a water sprinkler is activated in gardens and farms, the water released from the sprinkler falls directly to the ground. This downward motion of the water is a clear demonstration of gravity in action.

Debris flow

Gravity example - Debris flow
Gravity plays a crucial role in the occurrence of a debris flow, as loose debris is rapidly propelled downhill | Image: Pexels

When a landslide occurs, stones and other small debris start rolling down the hill. This downward movement of the debris is a clear demonstration of gravity in action. Gravity exerts a force on the stones and other small debris, causing them to move downward along the slope.

Floating paper

Gravity example - Floating paper
Gravity keeping a floating piece of paper grounded | Image: Stock photo

If a bundle of paper is tossed up into the air, the papers will separate and remain suspended for a while before eventually falling downward onto the floor. This downward motion of the papers clearly demonstrates the presence of gravity. Gravity pulls the papers towards the floor, causing them to descend from their elevated position in the air.

Stone

Gravity example - Stone
Gravity pulling a small stone back down after being thrown up | Image: Pixabay

Throwing a small stone up into the air on a beach is a clear example of gravity in action. The stone will naturally descend back towards the beach. It’s the force of gravity that pulls the stone downwards and guides its return to the Earth’s surface.

Shower water

Gravity example - Shower water
Gravity causing water to fall from a shower | Image: Pixabay

During a shower in the bathroom, the water released from the shower head can be observed gracefully falling to the floor. This phenomenon serves as a clear demonstration of the force of gravity. It is gravity that effortlessly pulls the water downwards, creating a gentle flow from the shower head to the floor.

Equation

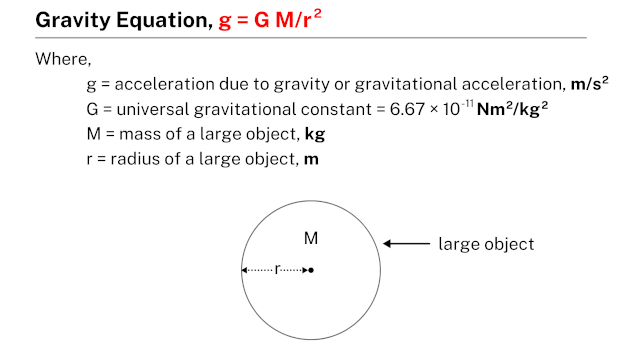
Gravity equation
Gravity equation | Image: Learnool

The gravity equation, g = GM/r2, states that the acceleration due to gravity (g) is equal to the product of the universal gravitational constant (G) and the mass (M) of the celestial body, divided by the square of the distance between the centers of mass (r). This equation enables the calculation of gravitational acceleration between two objects, utilizing their masses and the distance separating them. It is a fundamental equation in physics that helps in understanding the force of gravity acting between celestial bodies.

Practice problems

Problem #1

Calculate the value of gravitational acceleration on the surface of the Earth, given that the mass of the Earth is 5.972 × 1024 kg and the radius of the Earth is 6.378 × 103 km. Consider the universal gravitational constant as G = 6.67 × 10-11 Nm2/kg2.

Solution

Given data:

  • Gravitational acceleration on the surface of the Earth, g = ?
  • Mass of the Earth, M = 5.972 × 1024 kg
  • Radius of the Earth, r = 6.378 × 103 km = 6.378 × 106 m
  • Universal gravitational constant, G = 6.67 × 10-11 Nm2/kg2

Applying the formula:

  • g = GM/r2
  • g = (6.67 × 10-11 × 5.972 × 1024)/(6.378 × 106)2
  • g = (39.9 × 1013)/(40.7 × 1012)
  • g = 0.9803 × 10
  • g = 9.81 m/s2

Therefore, the gravitational acceleration on the surface of the Earth is 9.81 m/s2.

Problem #2

If the mass of Jupiter is 1.898 × 1027 kg and the radius of Jupiter is 69.911 × 103 km, calculate the value of gravitational acceleration on the surface of Jupiter. Take the value of the universal gravitational constant as G = 6.67 × 10-11 Nm2/kg2.

Solution

Given data:

  • Mass of the Jupiter, M = 1.898 × 1027 kg
  • Radius of the Jupiter, r = 69.911 × 103 km = 69.911 × 106 m
  • Gravitational acceleration on the surface of the Jupiter, g = ?
  • Universal gravitational constant, G = 6.67 × 10-11 Nm2/kg2

Applying the formula:

  • g = GM/r2
  • g = (6.67 × 10-11 × 1.898 × 1027)/(69.911 × 106)2
  • g = (12.7 × 1016)/(4887.6 × 1012)
  • g = 0.002598 × 104
  • g = 25.98 m/s2

Therefore, the gravitational acceleration on the surface of Jupiter is 25.98 m/s2.

Problem #3

What is the value of gravitational acceleration on the surface of Mars, given that the mass of Mars is 6.39 × 1023 kg and the radius of Mars is 3.3895 × 103 km? Consider the universal gravitational constant as G = 6.67 × 10-11 Nm2/kg2.

Solution

Given data:

  • Gravitational acceleration on the surface of Mars, g = ?
  • Mass of the Mars, M = 6.39 × 1023 kg
  • Radius of the Mars, r = 3.3895 × 103 km = 3.3895 × 106 m
  • Universal gravitational constant, G = 6.67 × 10-11 Nm2/kg2

Applying the formula:

  • g = GM/r2
  • g = (6.67 × 10-11 × 6.39 × 1023)/(3.3895 × 106)2
  • g = (42.7 × 1012)/(11.5 × 1012)
  • g = 3.71 m/s2

Therefore, the gravitational acceleration on the surface of Mars is 3.71 m/s2.

Problem #4

Calculate the value of gravitational acceleration on the surface of the Moon, with the mass of the Moon being 7.342 × 1022 kg and the radius of the Moon being 1.7371 × 103 km. Consider the universal gravitational constant as G = 6.67 × 10-11 Nm2/kg2.

Solution

Given data:

  • Gravitational acceleration on the surface of the Moon, g = ?
  • Mass of the Moon, M = 7.342 × 1022 kg
  • Radius of the Moon, r = 1.7371 × 103 km = 1.7371 × 106 m
  • Universal gravitational constant, G = 6.67 × 10-11 Nm2/kg2

Applying the formula:

  • g = GM/r2
  • g = (6.67 × 10-11 × 7.342 × 1022)/(1.7371 × 106)2
  • g = (48.9 × 1011)/(3 × 1012)
  • g =  16.3 × 10-1
  • g = 1.63 m/s2

Therefore, the gravitational acceleration on the surface of the Moon is 1.63 m/s2.

More topics

External links

Deep

Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.

Leave a Comment