Acceleration refers to the measure of how quickly an object’s velocity changes over time. It is defined as the rate of change of velocity. In simpler terms, acceleration represents the speed at which an object’s velocity is changing. When an object undergoes a change in velocity, either by increasing or decreasing its speed or by changing its direction, it is said to be accelerating. Acceleration can be positive, indicating an increase in velocity, or negative, indicating a decrease in velocity. The concept of acceleration helps us understand how objects respond to forces and how their motion changes with time.
Examples
Car speeding up

When a car speeds up, it undergoes acceleration. Acceleration is the term used to describe the rate at which an object’s velocity changes. In the case of a car, when it speeds up, its velocity increases gradually over time. This change in velocity is a result of an external force applied to the car, such as pressing down on the accelerator pedal. As a result of this applied force, the car experiences a positive acceleration, gains momentum, and moves faster in the chosen direction.
Car slowing down

When a car slows down, it experiences a negative acceleration. Acceleration is the rate at which an object’s velocity changes, and in the case of a car slowing down, its velocity decreases. This change in velocity is a result of an external force acting upon the car, such as applying the brakes. The force applied in the opposite direction of the car’s motion causes it to decelerate (negative acceleration). As the car decelerates, its speed gradually decreases, and it loses momentum.
Car taking a turn

When a car takes a turn, it experiences acceleration, which refers to how quickly its velocity changes. During a turn, the car’s velocity shifts in a different direction. While approaching the turn, the car usually maintains a steady speed. However, to alter its direction, the car must undergo acceleration. This change in velocity allows the car to navigate the turn smoothly.
Person walking

When a person starts walking, they undergo acceleration. This refers to the rate at which their velocity changes. Initially at a stationary position, the person’s velocity gradually increases as they apply a force with their legs against the ground. This acceleration enables them to transition from a resting state to a certain walking speed.
Person running

When a person starts running, they undergo acceleration, which describes the rate at which their velocity changes. Initially at a stationary position, the person’s velocity gradually increases as they exert a greater force with their legs against the ground compared to walking. This acceleration allows them to transition from a walking speed to a faster running speed. The increased force applied to the ground propels the person forward, causing their velocity to change and resulting in an accelerated movement.
Person jumping

When a person jumps from a certain height, they undergo acceleration. In the case of jumping, the person’s velocity initially decreases as they move upward against the force of gravity. As they reach the highest point of the jump, their velocity momentarily becomes zero before it starts increasing again as they descend back down. This change in velocity is a result of the acceleration due to gravity acting on the person’s body.
Person changing direction

When a person changes direction while moving, they undergo acceleration. In the case of changing direction, the person’s velocity changes as they apply a force in a different direction. For example, if a person is initially walking in a straight line and then suddenly makes a sharp turn to the left, their velocity will change as they accelerate towards the left. This change in velocity enables them to alter their path and move in the new direction. The person experiences acceleration during the change in direction due to the force they exert to redirect their motion.
Formula
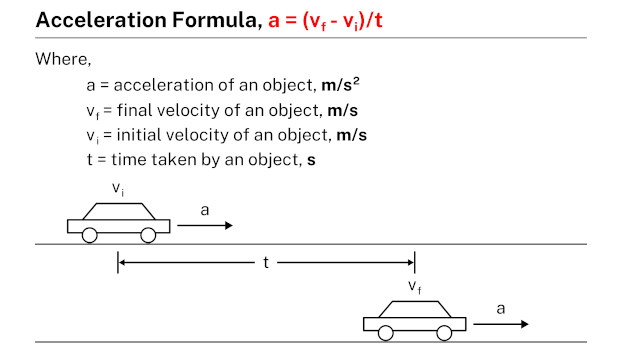
The acceleration formula describes the relationship between acceleration (a), change in velocity (Δv), and time (t). It states that acceleration is equal to the ratio of the change in velocity to the time taken. Mathematically, the formula for acceleration is given as a = (vf – vi)/t, where a represents acceleration, vf is the final velocity, vi is the initial velocity, and t is the time interval. This formula allows for the calculation of the acceleration of an object based on the given values of velocity change and time.
Practice problems
Problem #1
A car initially at rest accelerates to 24 m/s in 12 s. What is the acceleration of a car?
Solution
Given data:
- Initial velocity of a car, vi = 0 m/s
- Final velocity of a car, vf = 24 m/s
- Time taken by a car, t = 12 s
- Acceleration of a car, a = ?
Applying the formula:
- a = (vf – vi)/t
- a = (24 – 0)/12
- a = 24/12
- a = 2 m/s2
Therefore, the acceleration of a car is 2 m/s2.
Problem #2
An athlete accelerates from 5 m/s to 25 m/s in 5 s. Calculate the athlete’s acceleration.
Solution
Given data:
- Initial velocity of an athlete, vi = 5 m/s
- Final velocity of an athlete, vf = 25 m/s
- Time taken by an athlete, t = 5 s
- Acceleration of an athlete, a = ?
Applying the formula:
- a = (vf – vi)/t
- a = (25 – 5)/5
- a = 20/5
- a = 4 m/s2
Therefore, the acceleration of an athlete is 4 m/s2.
Problem #3
A bike traveling at 35 m/s comes to rest in 7 s when the brakes are applied. Calculate the bike’s deceleration.
Solution
Given data:
- Initial velocity of a bike, vi = 35 m/s
- Final velocity of a bike, vf = 0 m/s
- Time taken by a bike, t = 7 s
- Deceleration of a bike, a = ?
Applying the formula:
- a = (vf – vi)/t
- a = (0 – 35)/7
- a = (-35)/7
- a = -5 m/s2
Therefore, the deceleration of a bike is -5 m/s2.
Problem #4
A truck accelerates from 12 m/s to 24 m/s in 4 s. What is the truck’s acceleration?
Solution
Given data:
- Initial velocity of a truck, vi = 12 m/s
- Final velocity of a truck, vf = 24 m/s
- Time taken by a truck, t = 4 s
- Acceleration of a truck, a = ?
Applying the formula:
- a = (vf – vi)/t
- a = (24 – 12)/4
- a = 12/4
- a = 3 m/s2
Therefore, the acceleration of a truck is 3 m/s2.
More topics
External links
- How to Find Acceleration: Review and Examples – Albert
- Acceleration – Maths Is Fun
- What is acceleration? (article) – Khan Academy
- Acceleration | Definition, Formula & Examples – Study.com
- Acceleration – The Physics Classroom
- Acceleration – Wikipedia
- Average Acceleration: Definition, Formula, Examples and more – Phyley
- Acceleration | Physics – Lumen Learning
- Examples of ‘acceleration’ in a sentence – Collins Dictionary
- Acceleration | Definition, Facts, & Units – Britannica
- What are some good examples of acceleration related in real life – Quora
- Acceleration – Physics Tutorials
- Examples of acceleration – Cambridge Dictionary
- Acceleration Calculator | Definition | Formula – Omni Calculator
- Acceleration – Ducksters
- Accelerate Definition & Meaning – Merriam-Webster
- What are some examples of acceleration? – Socratic
Deep
Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.
