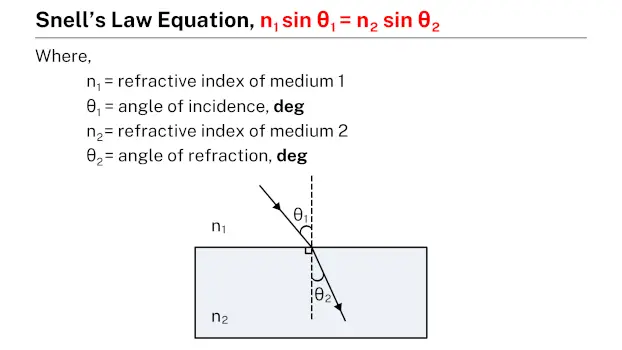
Snell’s law

The information on this page is ✔ fact-checked.

Snell’s law describes the relationship between the angles of incidence and refraction when a light wave passes from one medium into another with a different refractive index. According to Snell’s law, the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant and is equal to the ratio of the refractive indices of the two media. This law is fundamental in understanding how light bends, or refracts, when it enters a different medium. For example, when light passes from air (with a refractive index of approximately 1) into water (with a refractive index of about 1.33), it bends towards the normal due to the change in speed of light in the two different media.

Snell’s law is mathematically expressed as:

$$n_{1}sin\theta_{1} = n_{2}sin\theta_{2}$$

where n₁ and n₂ are the refractive indices of the first and second media, respectively, and θ₁ and θ₂ are the angles of incidence and refraction, respectively.

Practice problems

Problem #1

A ray of light moving through medium 1 with a refractive index of 1 enters medium 2 with a refractive index of 1.33. If the angle of incidence is 30°, what is the angle of refraction?

Solution

Given data:

• Refractive index of medium 1, n₁ = 1
• Refractive index of medium 2, n₂ = 1.33
• Angle of incidence, θ₁ = 30°
• Angle of refraction, θ₂ = ?

Applying the formula:

• n₁ sin θ₁ = n₂ sin θ₂
• 1 × sin (30°) = 1.33 × sin θ₂
• 1 × 0.5 = 1.33 × sin θ₂
• 0.5 = 1.33 × sin θ₂
• sin θ₂ = 0.3759
• θ₂ = sin^-1 (0.3759)
• θ₂ = 22.07°

Therefore, the angle of refraction is 22.07°.

Problem #2

A laser beam traveling through medium 1 has an angle of incidence of θ₁ = 40° and a refractive index of n₁ = 1.33. If the angle of refraction is θ₂ = 45°, calculate the refractive index of medium 2.

Solution

Given data:

• Angle of incidence, θ₁ = 40°
• Refractive index of medium 1, n₁ = 1.33
• Angle of refraction, θ₂ = 45°
• Refractive index of medium 2, n₂ = ?

Applying the formula:

• n₁ sin θ₁ = n₂ sin θ₂
• 1.33 × sin (40°) = n₂ × sin (45°)
• 1.33 × 0.6427 = n₂ × 0.7071
• n₂ = 0.8547 ÷ 0.7071
• n₂ = 1.20

Therefore, the refractive index of medium 2 is 1.20.

Problem #3

A ray traveling through medium 1 with a refractive index of n₁ = 1.3 enters medium 2 with a refractive index of n₂ = 1.4. Calculate the angle of incidence if the angle of refraction is 25°.

Solution

Given data:

• Refractive index of medium 1, n₁ = 1.3
• Refractive index of medium 2, n₂ = 1.4
• Angle of incidence, θ₁ = ?
• Angle of refraction, θ₂ = 25°

Applying the formula:

• n₁ sin θ₁ = n₂ sin θ₂
• 1.3 × sin θ₁ = 1.4 × sin (25°)
• 1.3 × sin θ₁ = 1.4 × 0.4226
• 1.3 × sin θ₁ = 0.5916
• sin θ₁ = 0.5961 ÷ 1.3
• sin θ₁ = 0.4585
• θ₁ = sin^-1 (0.4585)
• θ₁ = 27.29°

Therefore, the angle of incidence is 27.29°.

Problem #4

A light traveling through medium 1 with an unknown refractive index enters medium 2 with a refractive index of n₂ = 1.2. If the angle of incidence is 20° and the angle of refraction is 35°, what is the refractive index of medium 1?

Solution

Given data:

• Refractive index of medium 2, n₂ = 1.2
• Angle of incidence, θ₁ = 20°
• Angle of refraction, θ₂ = 35°
• Refractive index of medium 1, n₁ = ?

Applying the formula:

• n₁ sin θ₁ = n₂ sin θ₂
• n₁ × sin (20°) = 1.2 × sin (35°)
• n₁ × 0.3420 = 1.2 × 0.5735
• n₁ × 0.3420 = 0.6882
• n₁ = 0.6882 ÷ 0.3420
• n₁ = 2.01

Therefore, the refractive index of medium 1 is 2.01.

📝 Your feedback matters. Visit our contact page.

More topics

• Law of conservation of energy
• Newton’s law of universal gravitation
• Newton’s law of cooling
• Coulomb’s law
• Snell’s law
• Ohm’s law
• Hooke’s law

External links

• https://www.britannica.com/science/Snells-law
• https://www.physicsclassroom.com/class/refrn/Lesson-2/Snell-s-Law
• https://www.omnicalculator.com/physics/snells-law
• https://study.com/learn/lesson/what-is-snells-law-equation-examples.html
• https://www.studysmarter.us/explanations/physics/waves-physics/snells-law/