Tension (physics)

Updated on by

The information on this page is ✔ fact-checked.

Tension force formula
Tension force formula | Image: Learnool

In physics, tension is the force transmitted through a string, rope, cable, or any other type of flexible connector when it is pulled tight by forces acting from opposite ends. This force is directed along the length of the connector and pulls equally on the objects at either end. For example, when you hang a picture on a wall using a wire, the tension in the wire supports the picture’s weight and keeps it in place. Similarly, when two people play tug-of-war, the rope experiences tension as both sides pull on it. Tension is the opposite of compression, which is the force that pushes or squeezes material together. While tension pulls objects apart, compression pushes them together. Tension plays a vital role not only in engineering structures but also in everyday items like swings and elevators, ensuring their stability and functionality.

The tension can be calculated using different equations based on the forces acting on it and the specific motion or orientation of the system.

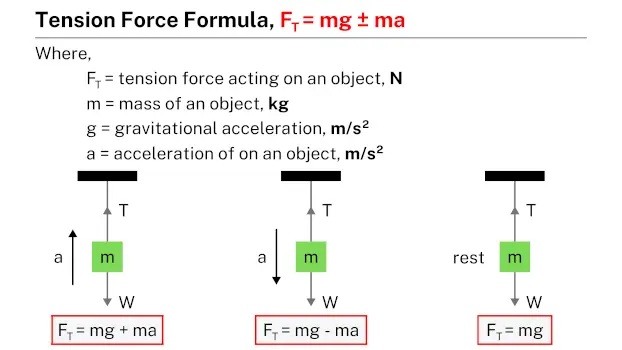
Vertical motion: In scenarios involving vertical motion, the tension depends on whether the object is at rest, accelerating upward, or accelerating downward.

When the object is stationary, the tension T is simply equal to the weight of the object, mg.

$$T = mg$$

where m represents the mass of the object and g denotes the acceleration due to gravity, which is approximately 9.81 m/s2 on the surface of the Earth.

If the object is accelerating upward with an acceleration a, the tension T is the sum of the weight of the object and the force required to accelerate it, mg + ma.

$$T = mg + ma$$

If the object is accelerating downward with an acceleration a, the tension T is the difference between the weight of the object and the force due to its deceleration, mg – ma.

$$T = mg – ma$$

Circular motion: In circular motion, the tension depends on whether the object is moving horizontally or vertically.

In horizontal circular motion, tension can act as the centripetal force required to keep an object moving along its circular path. This force always points towards the center of the circle, ensuring the object remains in its circular trajectory.

$$T = \frac{mv^{2}}{r}$$

where T is the tension in the string or rope, m is the mass of the object, v is the tangential velocity of the object, and r is the radius of the circular path.

In vertical circular motion, the tension changes based on the object’s position in its path. Specifically, the tension varies at the top, bottom, and sides (middle) of the circle.

At the top of the circle, the tension must provide enough centripetal force to maintain the circular motion while also counteracting the object’s weight.

$$T_{top} = \frac{mv^{2}}{r} – mg$$

where Ttop is the tension at the top, m is the mass of the object, v is the tangential velocity, r is the radius of the circle, and g is the acceleration due to gravity.

At the bottom of the circle, the tension must supply the centripetal force required for circular motion and also support the weight of the object.

$$T_{bottom} = \frac{mv^{2}}{r} + mg$$

where Tbottom is the tension at the bottom.

At the sides (or middle) of the circle, the tension solely needs to provide the centripetal force. In this position, the gravitational force, or weight, acts perpendicular to the tension, making no direct contribution to the centripetal force.

$$T_{middle} = \frac{mv^{2}}{r}$$

where Tmiddle is the tension at the sides.

Practice problems

Problem #1

A wooden block with a mass of 2 kg is hanging from a rope. If the block is assumed to be accelerating upward at a rate of 25 m/s2, calculate the tension force acting on the block. Take the value of gravitational acceleration, g, to be 9.81 m/s2.

Solution

Given data:

  • Mass of a wooden block, m = 2 kg
  • Acceleration of a wooden block, a = 25 m/s2
  • Tension force acting on a wooden block, FT = ?
  • Gravitational acceleration, g = 9.81 m/s2

Applying the formula, when an object is moving upward:

  • FT = mg + ma
  • FT = (2 × 9.81) + (2 × 25)
  • FT = 19.62 + 50
  • FT = 69.62 N

Therefore, the tension force acting on a wooden block is 69.62 N.

Problem #2

An 8 kg block is attached to a string and is accelerating downward at a rate of 5 m/s2. Determine the tension force acting on the block.

Solution

Given data:

  • Mass of a block, m = 8 kg
  • Acceleration of a block, a = 5 m/s2
  • Tension force acting on a block, FT = ?

Applying the formula, when an object is moving downward:

  • FT = mg – ma
  • FT = (8 × 9.81) – (8 × 5)
  • FT = 78.48 – 40
  • FT = 38.48 N

Therefore, the tension force acting on a block is 38.48 N.

Problem #3

What is the tension force acting on a rubber tire with a mass of 2 kg that is hanging from a rope? Assuming the rubber tire is stationary and not accelerating.

Solution

Given data:

  • Mass of a rubber tire, m = 2 kg
  • Tension force acting on a rubber tire, FT = ?

Applying the formula, when an object is at rest:

  • FT = mg
  • FT = 2 × 9.81
  • FT = 19.62 N

Therefore, the tension force acting on a rubber tire is 19.62 N.

Problem #4

Calculate the tension force acting on a 4 kg box in the following scenarios:
(a) When the box is moving upward with an acceleration of 8 m/s2.
(b) When the box is moving downward with an acceleration of 6 m/s2.
(c) When the box is at rest.

Solution

Given data:

  • Mass of a box, m = 4 kg
  • Tension force acting on a box, FT = ?

(a) When the box is moving upward with an acceleration of 8 m/s2

  • Acceleration of a box, a = 8 m/s2

Applying the formula, when an object is moving upward:

  • FT = mg + ma
  • FT = (4 × 9.81) + (4 × 8)
  • FT = 39.24 + 32
  • FT = 71.24 N

Therefore, the tension force acting on a box is 71.24 N.

(b) When the box is moving downward with an acceleration of 6 m/s2

  • Acceleration of a box, a = 6 m/s2

Applying the formula, when an object is moving downward:

  • FT = mg – ma
  • FT = (4 × 9.81) – (4 × 6)
  • FT = 39.24 – 24
  • FT = 15.24 N

Therefore, the tension force acting on a box is 15.24 N.

(c) When the box is at rest

Applying the formula, when an object is at rest:

  • FT = mg
  • FT = 4 × 9.81
  • FT = 39.24 N

Therefore, the tension force acting on a box is 39.24 N.

More topics

External links

Deep

Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.

Leave a Comment