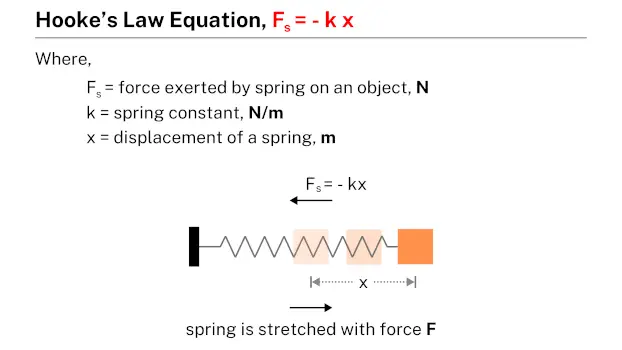
Hooke’s law explains how elastic materials, like springs, behave when forces are applied to them. It states that the force needed to stretch or compress a spring is directly proportional to the distance the spring is stretched or compressed. For example, if you pull on a spring, it stretches proportionally to the force you apply; similarly, if you compress it, the displacement is proportional to the compressive force. Hooke’s law is fundamental in understanding how materials deform under various forces and is crucial in fields like mechanical engineering, structural analysis, and materials science. It helps in designing systems and components that can withstand specific forces without permanent deformation.
Hooke’s law is mathematically expressed as:
$$F = -kx$$where F is the force exerted by the spring, k is the spring constant (a measure of the spring’s stiffness), and x is the displacement from the spring’s equilibrium position. The negative sign indicates that the force exerted by the spring is in the opposite direction of the displacement, working to return the spring to its natural length.
Practice problems
Problem #1
Find the force required to stretch a spring with a displacement of 60 cm. Use a spring constant value of k = 85 N/m.
Solution
Given data:
- Force needed to stretch a spring, F = ?
- Displacement of a spring, x = 60 cm = 0.6 m
- Spring constant, k = 85 N/m
Applying the formula:
- Fs = – k x
The negative sign in the equation indicates that the spring force acts in the opposite direction to the displacement. In this problem, the focus is on determining the magnitude of the force rather than its direction, so the negative sign can be ignored.
- F = k x
- F = (85 × 0.6)
- F = 51 N
Therefore, the force needed to stretch a spring is 51 N.
Problem #2
Calculate the force needed to compress a spring with a displacement of 20 cm. Use a spring constant value of k = 150 N/m.
Solution
Given data:
- Force needed to compress a spring, F = ?
- Displacement of a spring, x = 20 cm = 0.2 m
- Spring constant, k = 150 N/m
Applying the formula:
- Fs = – k x
The negative sign in the equation indicates that the spring force acts in the opposite direction to the displacement. In this problem, the focus is on determining the magnitude of the force rather than its direction, so the negative sign can be ignored.
- F = k x
- F = (150 × 0.2)
- F = 30 N
Therefore, the force needed to compress a spring is 30 N.
Problem #3
What force is necessary to stretch a spring to a distance of 40 cm? Take the spring constant value as k = 120 N/m.
Solution
Given data:
- Force needed to stretch a spring, F = ?
- Displacement of a spring, x = 40 cm = 0.4 m
- Spring constant, k = 120 N/m
Applying the formula:
- Fs = – k x
The negative sign in the equation indicates that the spring force acts in the opposite direction to the displacement. In this problem, the focus is on determining the magnitude of the force rather than its direction, so the negative sign can be ignored.
- F = k x
- F = (120 × 0.4)
- F = 48 N
Therefore, the force needed to stretch a spring is 48 N.
Problem #4
Determine the force needed to compress a spring with a displacement of 25 cm. Take the spring constant value as k = 65 N/m.
Solution
Given data:
- Force needed to compress a spring, F = ?
- Displacement of a spring, x = 25 cm = 0.25 m
- Spring constant, k = 65 N/m
Applying the formula:
- Fs = – k x
The negative sign in the equation indicates that the spring force acts in the opposite direction to the displacement. In this problem, the focus is on determining the magnitude of the force rather than its direction, so the negative sign can be ignored.
- F = k x
- F = (65 × 0.25)
- F = 16.25 N
Therefore, the force needed to compress a spring is 16.25 N.
More topics
- Law of conservation of energy
- Newton’s law of universal gravitation
- Newton’s law of cooling
- Coulomb’s law
- Snell’s law
- Ohm’s law
- Hooke’s law
External links
- https://www.britannica.com/science/Hookes-law
- https://www.calculatorsoup.com/calculators/physics/hookes-law.php
- https://study.com/academy/lesson/hookes-law-the-spring-constant-definition-equation.html
- https://www.dummies.com/article/academics-the-arts/science/physics/how-to-calculate-a-spring-constant-using-hookes-law-174221/
Deep
Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.
