Boyle’s law states that, at a constant temperature, the pressure of a fixed amount of gas is inversely proportional to its volume. This means that as the volume of the gas decreases, its pressure increases, and as its volume increases, its pressure decreases.
Examples
Syringe
When the plunger of a syringe is pressed, the volume of the fluid inside the syringe decreases and the pressure of the fluid increases, following Boyle’s law. This causes the medication or fluid inside the syringe to be forced out of the needle.
Bicycle pump

Boyle’s law is demonstrated when a bicycle tire is inflated using a bicycle pump. As the air inside the pump is compressed into a smaller volume, the air pressure increases. This increase in air pressure causes the tire to become firm and able to support the weight of the rider.
Spray

When the cap of a body spray is pressed with the finger, the volume of the gas inside the can decreases and the pressure of the gas increases, following Boyle’s law. This causes the gas to be forced out of the nozzle and into the air.
Respiration

When we inhale and exhale during the respiration process, the volume of the air inside our lungs changes and the pressure of the air changes, following Boyle’s law. When we inhale, the volume of the lungs increases and the pressure of the air inside the lungs decreases. When we exhale, the volume of the lungs decreases and the pressure of the air inside the lungs increases.
Scuba diving

When a scuba diver goes deep underwater, the pressure of the water around them increases, which can cause the volume of air in their lungs to decrease. This happens because the gas in their lungs (which is air) gets squeezed due to the increased pressure. This is an example of Boyle’s law, which says that if you squeeze a gas in a closed space, its volume will get smaller.
If the scuba diver ascends too quickly (swims to the surface too fast), the pressure of the water around them will decrease rapidly. According to Boyle’s law, the volume of air in their lungs will then try to increase rapidly to balance the pressure, which can cause the air to expand too quickly. This is dangerous because if the air expands too quickly, it can cause problems for the diver, such as decompression sickness or other injuries. To prevent this, scuba divers need to ascend slowly and take breaks to allow their body to adjust to the changes in pressure.
Deep-sea fish

When a deep-sea fish swims at different depths, the swim bladder inside its body expands or contracts to adjust its buoyancy in the water.
When a deep-sea fish is brought up to the surface of the ocean, the pressure of the water around it decreases. This causes the volume of air inside the fish’s swim bladder to increase, following Boyle’s law, which states that if you decrease the pressure of a gas in a closed space, its volume will increase.
If a deep-sea fish is brought up to the surface of the ocean too quickly, the sudden expansion of the swim bladder can cause the fish to experience buoyancy problems, which can lead to injury or even death. To prevent this, fishermen use tools like “descender devices” to help the fish adjust to the change in pressure slowly. These devices allow the fish to be returned to the depth from where it was caught, so the swim bladder can slowly return to its normal size. This helps the fish avoid buoyancy problems and ensures their survival.
Air bubbles

When air bubbles rise up in water, they experience a decrease in the surrounding water pressure. According to Boyle’s law, the volume of the air in the bubbles increases as the pressure decreases, which causes the bubbles to expand as they rise towards the surface of the water.
Formula
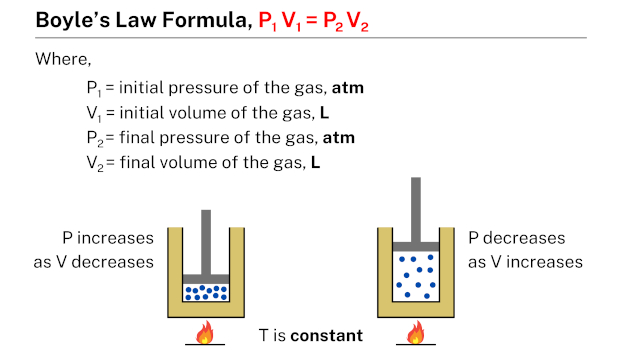
The Boyle’s law formula, which is succinctly expressed as P1 V1 = P2 V2, describes the relationship between the pressure and volume of a given quantity of gas. In this formula, P1 and V1 represent the initial pressure and volume of the gas, while P2 and V2 represent the final pressure and volume, respectively. This formula is useful in calculating the pressure or volume of a gas under different conditions, given the initial pressure and volume of the gas.
Practice problems
Problem #1
A helium gas occupies a volume of 2 L at a pressure of 5 atm. Calculate the final volume of the gas if the pressure is increased to 10 atm.
Solution
Given data:
- Initial volume of the gas, V1 = 2 L
- Initial pressure of the gas, P1 = 5 atm
- Final volume of the gas, V2 = ?
- Final pressure of the gas, P2 = 10 atm
Applying the formula:
- P1 V1 = P2 V2
- 5 × 2 = 10 × V2
- V2 = 1 L
Therefore, the final volume of the gas is 1 L.
Problem #2
A balloon is filled with 3 L of helium gas at a pressure of 12 atm. If the volume of the gas increases to 6 L, calculate the final pressure of the gas.
Solution
Given data:
- Initial volume of the gas, V1 = 3 L
- Initial pressure of the gas, P1 = 12 atm
- Final volume of the gas, V2 = 6 L
- Final pressure of the gas, P2 = ?
Applying the formula:
- P1 V1 = P2 V2
- 12 × 3 = P2 × 6
- P2 = 6 atm
Therefore, the final pressure of the gas is 6 atm.
Problem #3
A large container initially contains a few liters of hydrogen gas at a pressure of 2 atm. When the gas is released into a small container, it occupies a volume of 5 L at a pressure of 8 atm. Calculate the initial volume of the gas.
Solution
Given data:
- Initial pressure of the gas, P1 = 2 atm
- Final volume of the gas, V2 = 5 L
- Final pressure of the gas, P2 = 8 atm
- Initial volume of the gas, V1 = ?
Applying the formula:
- P1 V1 = P2 V2
- 2 × V1 = 8 × 5
- 2 × V1 = 40
- V1 = 20 L
Therefore, the initial volume of the gas is 20 L.
Problem #4
A container initially contains 12 L of argon gas at an unknown pressure. When released into a small container, the gas occupies a volume of 2 L at a pressure of 6 atm. Calculate the initial pressure of the gas.
Solution
Given data:
- Initial volume of the gas, V1 = 12 L
- Final volume of the gas, V2 = 2 L
- Final pressure of the gas, P2 = 6 atm
- Initial pressure of the gas, P1 = ?
Applying the formula:
- P1 V1 = P2 V2
- P1 × 12 = 6 × 2
- P1 = 1 atm
Therefore, the initial pressure of the gas is 1 atm.
Related
More topics
- Boyle’s law
- Charles’s law
- Gay-Lussac’s law
- Avogadro’s law
- Ideal gas law
- Dalton’s law
- Henry’s law
- Combined gas law
- Graham’s law
External links
- Boyle’s law – Wikipedia
- Boyle’s law | Definition, Equation, & Facts – Britannica
- Animated Boyle’s Law – NASA (.gov)
- Boyle’s Law Calculator – Omni Calculator
- Physiology, Boyle’s Law – StatPearls – National Institutes of Health (.gov)
- 14.3: Boyle’s Law – Chemistry LibreTexts
- Boyle’s Law – Clippard
- What Is Boyle’s Law and Why Do I Already Know It? – HowStuffWorks
- Boyle’s Law – Let’s Talk Science
- Boyle’s Law — Overview & Formula – Expii
- Boyle’s Law Definition in Chemistry – ThoughtCo
- Gas Laws – Florida State University
- Boyle’ Law – University of Pennsylvania – School of Arts & Sciences
- Gas Law – Boyle’s Law – ChemTeam
- Boyle’s Law – CK-12
- Solving Applications of Boyle’s Gas Law – Study.com
- Boyle’s Law | Understanding Gas Laws – ChemTalk
Deep
Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.
