Gay-Lussac’s law

The information on this page is ✔ fact-checked.

Gay-Lussac’s law, also known as the pressure-temperature law, states that the pressure of a fixed amount of gas at a constant volume is directly proportional to its absolute temperature. In other words, as the temperature of a gas increases, so does its pressure, and vice versa, provided that the volume of the gas remains constant.

Examples

Gas cylinder

When a gas cylinder is pressurized, the gas molecules are tightly packed together and have a certain temperature. According to Gay-Lussac’s law, the pressure of a gas increases with an increase in temperature, assuming the volume remains constant. If the gas cylinder is heated, the temperature of the gas inside will increase and cause an increase in pressure. If the pressure becomes too high, it can lead to an explosion, which is why it’s important to handle pressurized gas cylinders with care.

Pressure cooker

The temperature and pressure inside a pressure cooker are directly related, as per Gay-Lussac’s law. As the temperature rises, the pressure inside the cooker also increases. This higher pressure leads to a higher boiling point of the water, allowing food to cook faster.

Bullet

When a bullet is fired from a gun, the gunpowder inside the bullet casing is ignited, producing a large amount of gas. As per Gay-Lussac’s law, the pressure of the gas is directly proportional to its temperature. Therefore, the high temperature of the gas produced by the gunpowder increases the pressure inside the bullet casing, propelling the bullet out of the gun barrel.

Tire tube

When a vehicle is driven, the friction between the tire and the road generates heat. This heat is transferred to the air inside the tire, increasing its temperature. As per Gay-Lussac’s law, the pressure of the gas inside the tire increases with temperature. Therefore, the pressure inside the tire also increases, which can lead to overinflation or a blowout if the pressure becomes too high.

Heater filament

In a water heater, the electric filament heats up the water. As the temperature of the water increases, the pressure of the steam generated by the hot water also increases. According to Gay-Lussac’s law, the pressure of the gas is directly proportional to its temperature, so the pressure inside the water heater increases. If the pressure becomes too high, it can cause an explosion.

Formula

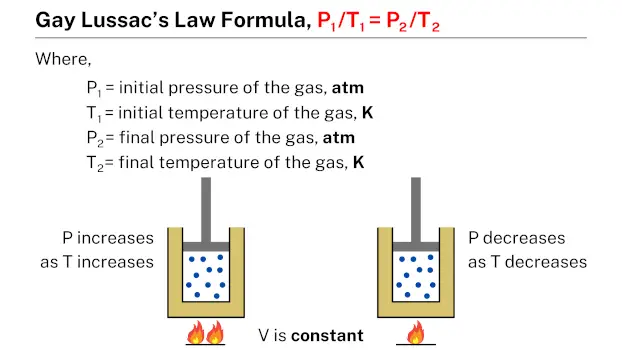
Gay-Lussac’s law formula, which is expressed as P₁/T₁ = P₂/T₂, relates the pressure and temperature of a gas. In this formula, P₁ and T₁ represent the initial pressure and temperature of the gas, while P₂ and T₂ represent the final pressure and temperature, respectively. This formula can be used to calculate the pressure or temperature of a gas under different conditions, given the initial pressure and temperature of the gas.

Practice problems

Problem #1

A gas cylinder contains hydrogen gas at a pressure of 2 atm and a temperature of 20 ℃. What is the final pressure of the gas when the temperature of the cylinder is increased to 60 ℃?

Solution

Given data:

• Initial pressure of the gas, P₁ = 2 atm
• Initial temperature of the gas, T₁ = 20 ℃ = 293 K
• Final pressure of the gas, P₂ = ?
• Final temperature of the gas, T₂ = 60 ℃ = 333 K

Applying the formula:

• P₁/T₁ = P₂/T₂
• P₂ = (P₁ × T₂) ÷ T₁
• P₂ = (2 × 333) ÷ 293
• P₂ = 666 ÷ 293
• P₂ = 2.27 atm

Therefore, the final pressure of the gas is 2.27 atm.

Problem #2

A large balloon contains helium gas at a pressure of 5 atm. If the temperature of the gas increases to 90 ℃, the pressure of the gas increases to 6 atm. What was the initial temperature of the gas?

Solution

Given data:

• Initial pressure of the gas, P₁ = 5 atm
• Final temperature of the gas, T₂ = 90 ℃ = 363 K
• Final pressure of the gas, P₂ = 6 atm
• Initial temperature of the gas, T₁ = ?

Applying the formula:

• P₁/T₁ = P₂/T₂
• T₁ = (P₁ × T₂) ÷ P₂
• T₁ = (5 × 363) ÷ 6
• T₁ = 1815 ÷ 6
• T₁ = 302.5 K = 29.5 ℃

Therefore, the initial temperature of the gas is 29.5 ℃.

Problem #3

A cylinder is filled with argon gas at a temperature of 25 ℃. When the temperature is increased to 80 ℃, the pressure of the gas increases to 12 atm. What was the initial pressure of the gas?

Solution

Given data:

• Initial temperature of the gas, T₁ = 25 ℃ = 298 K
• Final temperature of the gas, T₂ = 80 ℃ = 353 K
• Final pressure of the gas, P₂ = 12 atm
• Initial pressure of the gas, P₁ = ?

Applying the formula:

• P₁/T₁ = P₂/T₂
• P₁ = (P₂ × T₁) ÷ T₂
• P₁ = (12 × 298) ÷ 353
• P₁ = 3576 ÷ 353
• P₁ = 10.13 atm

Therefore, the initial pressure of the gas is 10.13 atm.

Problem #4

A container is filled with hydrogen gas at a pressure of 3 atm and a temperature of 30 ℃. If the pressure of the gas is increased to 4 atm, what is the final temperature of the gas?

Solution

Given data:

• Initial pressure of the gas, P₁ = 3 atm
• Initial temperature of the gas, T₁ = 30 ℃ = 303 K
• Final pressure of the gas, P₂ = 4 atm
• Final temperature of the gas, T₂ = ?

Applying the formula:

• P₁/T₁ = P₂/T₂
• T₂ = (P₂ × T₁) ÷ P₁
• T₂ = (4 × 303) ÷ 3
• T₂ = 1212 ÷ 3
• T₂ = 404 K = 131 ℃

Therefore, the final temperature of the gas is 131 ℃.

📝 Your feedback matters. Visit our contact page.

Related

• Gas laws

More topics

• Boyle’s law
• Charles’s law
• Gay-Lussac’s law
• Avogadro’s law
• Ideal gas law
• Dalton’s law
• Henry’s law
• Combined gas law
• Graham’s law

External links

• 14.5: Gay-Lussac’s Law – Chemistry LibreTexts
• Gay-Lussac’s law – Wikipedia
• Gay Lussac’s Law – ChemTalk
• Gay-Lussac’s Gas Law | Equation and Examples – Study.com
• Gay-Lussac’s Law — Overview & Formula – Expii
• Gay-Lussac’s Law Calculator – Omni Calculator
• Charles and Gay-Lussac’s Law – NASA (.gov)
• Gay-Lussac’s Gas Law Examples – ThoughtCo
• Gas Laws – Florida State University
• Gay-Lussac’s Law Flashcards – Quizlet
• Gay-Lussac’s Law Discussion and Ten Examples – ChemTeam
• Charles’ Law and Gay-Lussac’s Law – Let’s Talk Science
• Law of Combining Volumes (Joseph Louis Gay-Lussac) – Purdue University
• High School Chemistry : Using Gay-Lussac’s Law – Varsity Tutors
• Gay-Lussac’s Law – CK-12
• Gay-Lussac’s law of combining volumes | physical science – Britannica
• What does Gay Lussac’s law state? – Socratic
• Gay-Lussac’s Law – Definition, Formula, Examples – Science Notes and Projects