The information on this page is ✔ fact-checked.
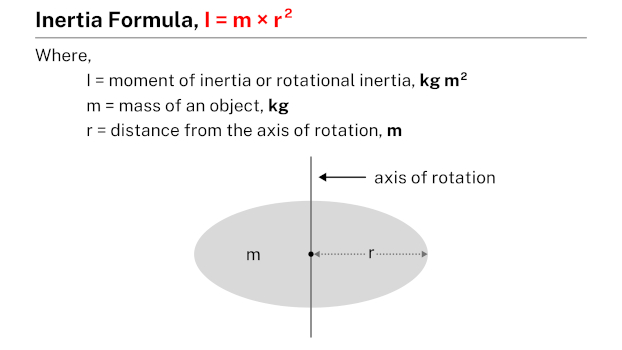
Moment of inertia, also known as rotational inertia, is a measure of an object’s resistance to rotational motion. It depends on the object’s mass distribution. The moment of inertia of a point mass rotating around an axis at a distance r is given by the formula I = m × r2, where m represents the mass of the object.
For objects with more complex shapes or mass distributions, different formulas are used to determine their moment of inertia. For instance, a solid cylinder’s moment of inertia is given by I = ½ (m × r2). Another example is the moment of inertia for a solid sphere, which is given by I = ⅖ (m × r2), where r represents the radius of the sphere. Other shapes have their own unique formulas for calculating moment of inertia.
Practice problems
Problem #1
An object with a mass of 4 kg is rotating around an axis at a distance of 5 meters. Calculate the moment of inertia of the object.
Solution
Given data:
- Mass of the object, m = 4 kg
- Distance from the axis of rotation, r = 5 m
- Moment of inertia of the object, I = ?
Applying the formula:
- I = m × r2
- I = 4 × (5)2
- I = 4 × 25
- I = 100 kg m2
Therefore, the moment of inertia of the object is 100 kg m2.
Problem #2
A solid cylinder with a mass of 6 kg is rotating about its central axis. The cylinder has a radius of 2 meters. Determine the moment of inertia of the cylinder.
Solution
Given data:
- Mass of the cylinder, m = 6 kg
- Distance from the axis of rotation, r = 2 m
- Moment of inertia of the cylinder, I = ?
Applying the formula, for moment of inertia of the solid cylinder:
- I = ½ (m × r2)
- I = ½ (6 × 22)
- I = ½ (6 × 4)
- I = ½ (24)
- I = 12 kg m2
Therefore, the moment of inertia of the cylinder is 12 kg m2.
Problem #3
A solid sphere with a mass of 2 kg is rotating about its central axis. The sphere has a radius of 5 meters. Determine the moment of inertia of the sphere.
Solution
Given data:
- Mass of the sphere, m = 2 kg
- Distance from the axis of rotation, r = 5 m
- Moment of inertia of the sphere, I = ?
Applying the formula, for moment of inertia of the sphere:
- I = ⅖ (m × r2)
- I = ⅖ (2 × 52)
- I = ⅖ (2 × 25)
- I = ⅖ (50)
- I = 2 × 10
- I = 20 kg m2
Therefore, the moment of inertia of the sphere is 20 kg m2.
Problem #4
Two balls, A and B, with masses of 2 kg and 5 kg respectively, are connected by a rod of length 5 m. The system rotates about the axis CD. The distances of balls A and B from the axis of rotation are 2 m and 3 m respectively. Calculate the moment of inertia of the system about the axis CD.
Solution
Given data:
- Mass of the ball A, mA = 2 kg
- Mass of the ball B, mB = 5 kg
- Distance of the ball 1 from the axis of rotation, rA = 2 m
- Distance of the ball 2 from the axis of rotation, rB = 3 m
- Moment of inertia of the system, I = ?
Applying the formula, for moment of inertia of the sphere:
- I = (mA × rA2) + (mB × rB2)
- I = (2 × 22) + (5 × 32)
- I = (2 × 4) + (5 × 9)
- I = 8 + 45
- I = 53 kg m2
Therefore, the moment of inertia of the system is 53 kg m2.
Related
More topics
- Free fall equation
- Air resistance formula
- Terminal velocity equation
- Gravity equation
- Inertia formula
- Acceleration formula
- Momentum equation
- Mass formula
- Velocity formula
- Pressure equation
- Kinematic equations
- Friction equation
External links
- http://hyperphysics.phy-astr.gsu.edu/hbase/mi.html
- https://www.thoughtco.com/moment-of-inertia-formulas-2698806
- https://study.com/learn/lesson/law-of-inertia.html
- https://www.studysmarter.us/explanations/physics/engineering-physics/moment-of-inertia/
Deep
Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.
