Avogadro’s law

The information on this page is ✔ fact-checked.

Avogadro’s law states that the volume and amount of gas are directly proportional at constant temperature and pressure. This law, attributed to the Italian scientist Amedeo Avogadro, asserts that “equal volumes of gases at the same temperature and pressure contain equal numbers of molecules.” It illustrates the direct relationship between the volume of a gas and the amount of substance present. This fundamental principle allows scientists to predict how gases will behave under different conditions and is essential in various fields, including chemistry and physics.

Formula

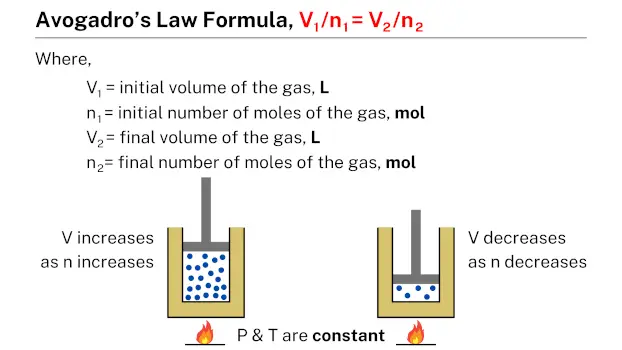
Avogadro’s law formula, expressed as V₁/n₁ = V₂/n₂, establishes a relationship between the volume of a given quantity of gas and its number of moles. In this formula, V₁ and n₁ represent the initial volume and number of moles of the gas, while V₂ and n₂ represent the final volume and number of moles, respectively. This formula can be used to calculate the volume or number of moles of a gas under different conditions, given the initial volume and number of moles of the gas.

Practice problems

Problem #1

A rubber ball contains 5 L of gas with 0.4 moles of helium at a given temperature and pressure. Determine the final volume of the gas when an additional 2 moles of helium are added to the rubber ball.

Solution

Given data:

• Initial volume of the gas, V₁ = 5 L
• Initial number of moles of the gas, n₁ = 0.4 mol
• Final volume of the gas, V₂ = ?
• Final number of moles of the gas, n₂ = 0.4 mol + 2 mol = 2.4 mol

Applying the formula:

• V₁/n₁ = V₂/n₂
• V₂ = (V₁ × n₂) ÷ n₁
• V₂ = (5 × 2.4) ÷ 0.4
• V₂ = 12 ÷ 0.4
• V₂ = 30 L

Therefore, the final volume of the gas is 30 L.

Problem #2

A tube contains 6 L of gas with 0.8 moles of hydrogen gas at a certain temperature and pressure. Find the final number of moles of gas when the volume of the gas increases to 12 L.

Solution

Given data:

• Initial volume of the gas, V₁ = 6 L
• Initial number of moles of the gas, n₁ = 0.8 mol
• Final number of moles of the gas, n₂ = ?
• Final volume of the gas, V₂ = 12 L

Applying the formula:

• V₁/n₁ = V₂/n₂
• n₂ = (n₁ × V₂) ÷ V₁
• n₂ = (0.8 × 12) ÷ 6
• n₂ = 0.8 × 2
• n₂ = 1.6 mol

Therefore, the final number of moles of the gas is 1.6 mol.

Problem #3

A container is filled with a few liters of gas containing 0.7 moles of helium gas. If the volume of the gas is increased to 9 L and an additional 1.2 moles of argon gas are added to the container, then what was the initial volume of the gas?

Solution

Given data:

• Initial number of moles of the gas, n₁ = 0.7 mol
• Final volume of the gas, V₂ = 9 L
• Final number of moles of the gas, n₂ = 0.7 mol + 1.2 mol = 1.9 mol
• Initial volume of the gas, V₁ = ?

Applying the formula:

• V₁/n₁ = V₂/n₂
• V₁ = (V₂ × n₁) ÷ n₂
• V₁ = (9 × 0.7) ÷ 1.9
• V₁ = 6.3 ÷ 1.9
• V₁ = 3.31 L

Therefore, the initial volume of the gas is 3.31 L.

Problem #4

A balloon is initially filled with 3 L of gas containing some moles of argon gas. If the volume of the gas is increased to 9 L and an additional 3 moles of argon gas are added to the balloon, what was the initial number of moles of the gas?

Solution

Given data:

• Initial volume of the gas, V₁ = 3 L
• Final volume of the gas, V₂ = 9 L
• Final number of moles of the gas, n₂ = 3 mol
• Initial number of moles of the gas, n₁ = ?

Applying the formula:

• V₁/n₁ = V₂/n₂
• n₁ = (V₁ × n₂) ÷ V₂
• n₁ = (3 × 3) ÷ 9
• n₁ = 9 ÷ 9
• n₁ = 1 mol

Therefore, the initial number of moles of the gas is 1 mol.

📝 Your feedback matters. Visit our contact page.

Related

• Gas laws

More topics

• Boyle’s law
• Charles’s law
• Gay-Lussac’s law
• Avogadro’s law
• Ideal gas law
• Dalton’s law
• Henry’s law
• Combined gas law
• Graham’s law

External links

• Avogadro’s law | Definition, Explanation, & Facts – Britannica
• Avogadro’s law – Wikipedia
• 14.7: Avogadro’s Law – Chemistry LibreTexts
• What Is Avogadro’s Law? Definition and Example – ThoughtCo
• Avogadro’s Law Calculator • Thermodynamics — Heat – Translators Cafe
• Avogadro’s Law — Overview & Formula – Expii
• Avogadro’s Law Calculator – SensorsONE
• Avogadro and the Ideal Gas Law – Let’s Talk Science
• Gas Law – Avogadro’s Law – ChemTeam
• Avogadro’s Law & Molar Volume | Overview, Formula & Units – Study.com
• Avogadro’s Law Made Easy | Understanding Gas Laws – ChemTalk
• Ideal Gas Behavior: Avogadro’s Law – Texas Gateway
• Avogadro’s Law: Definition, Formula, Equation and Examples – Science ABC
• High School Chemistry : Using Avogadro’s Law – Varsity Tutors
• Avogadro’s Law – CK-12
• What is Avogadro’s Law? + Example – Socratic