The information on this page is ✔ fact-checked.
Charles’s law states that, at constant pressure, the volume of a given quantity of gas is directly proportional to its absolute temperature. This means that as the temperature of the gas increases, its volume increases, and as the temperature of the gas decreases, its volume decreases.
Examples
Hot air balloon
Charles’s law is seen when a hot air balloon is lifted up in the air, by heating the air inside a balloon. Heating the air increases its temperature and thus its volume, making it less dense than the surrounding air, which causes the balloon to rise.
Basketball
When a basketball is taken outside on a cold day, it shrinks in size due to Charles’s law. As the temperature decreases, the volume of the gas inside the basketball also decreases. This decrease in volume causes the basketball to become less inflated and smaller in size.
Helium balloon
Charles’s law can be observed with an inflated helium balloon, which follows a pattern of volume change with temperature. When the balloon is taken outside on a hot day, the temperature causes the helium molecules inside to move faster and occupy more space. This leads to an increase in the volume of the balloon, causing it to become more inflated and larger in size. Conversely, if the same balloon is taken outside on a cold day, the lower temperature causes the helium molecules to slow down and occupy less space, resulting in a decrease in the volume of the balloon.
Car tire
Charles’s law can be observed in the behavior of car tires on different temperature conditions. When the weather is cold, the air inside the tire contracts, causing the volume to decrease and resulting in lower tire pressure or deflation. Conversely, in hot weather, the air inside the tire expands due to higher temperature, causing the volume to increase and resulting in higher tire pressure or inflation.
Jogging
When it is difficult to jog in cold weather, it is due to Charles’s law. As the temperature decreases, the volume of air in the lungs also decreases, making it more difficult to breathe.
Baking
Charles’s law can be observed in the process of making bakery products fluffy and spongy through the use of yeast fermentation. When yeast is added to dough, it undergoes fermentation and produces carbon dioxide gas as a byproduct. During the baking process, the heat causes the gas to expand, leading to an increase in the volume of the dough. As a result, the bakery product becomes fluffy and light, making it more appetizing to eat.
Pop-up timer
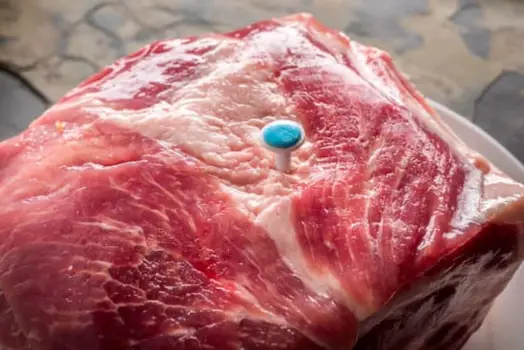
Charles’s law can be observed in the functioning of a pop-up timer placed inside beef. The timer is designed to pop up when the internal temperature of the beef reaches a certain level. This increase in temperature causes the gas inside the timer to expand according to Charles’s law, which ultimately triggers the timer to pop up.
Deodorant
The behavior of a deodorant spray bottle in bright sunlight is an example of Charles’s law. As the temperature increases, the volume of the gas inside the bottle also increases, exerting pressure on the container. If the pressure exceeds the container’s capacity, it can burst.
Pool float
Charles’s law is seen when a pool float gets over-inflated in summer and under-inflated in winter. The temperature of the air inside the pool float affects its volume according to Charles’s law. In hot temperatures, the air expands and can cause the pool float to become over-inflated, while in cold temperatures, the air contracts and can cause the pool float to become under-inflated.
Table tennis ball
Charles’s law can be observed when a dented table tennis ball is placed in warm water. As per this law, the volume of a gas increases with an increase in temperature, and the same applies to the air molecules inside the ball. When the ball is immersed in warm water, the air inside it expands, and the increased pressure can push out the dent and restore the ball’s original shape.
Formula
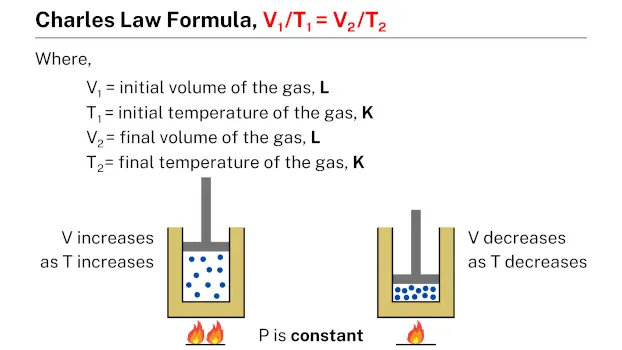
The Charles’s law formula, which is expressed as V1/T1 = V2/T2, relates the volume and temperature of a gas. In this formula, V1 and T1 represent the initial volume and temperature of the gas, while V2 and T2 represent the final volume and temperature, respectively. This formula can be used to calculate the volume or temperature of a gas under different conditions, given the initial volume and temperature of the gas.
Practice problems
Problem #1
A rubber ball contains 2 L of hydrogen gas at an initial temperature of 10 ℃. Calculate the final volume of the gas if the temperature is increased to 90 ℃, according to Charles’s law.
Solution
Given data:
- Initial volume of the gas, V1 = 2 L
- Initial temperature of the gas, T1 = 10 ℃ = 283 K
- Final volume of the gas, V2 = ?
- Final temperature of the gas, T2 = 90 ℃ = 363 K
Applying the formula:
- V1/T1 = V2/T2
- V2 = (V1 × T2) ÷ T1
- V2 = (2 × 363) ÷ 283
- V2 = 726 ÷ 283
- V2 = 2.56 L
Therefore, the final volume of the gas is 2.56 L.
Problem #2
A rubber ball is filled with 3 L of helium gas at a temperature of 12 ℃. If the volume of the gas changes to 4 L, what is the final temperature of the gas?
Solution
Given data:
- Initial volume of the gas, V1 = 3 L
- Initial temperature of the gas, T1 = 12 ℃ = 285 K
- Final volume of the gas, V2 = 4 L
- Final temperature of the gas, T2 = ?
Applying the formula:
- V1/T1 = V2/T2
- T2 = (V2 × T1) ÷ V1
- T2 = (4 × 285) ÷ 3
- T2 = 1140 ÷ 3
- T2 = 380 K = 107 ℃
Therefore, the final temperature of the gas is 107 ℃.
Problem #3
A container is filled with a few liters of hydrogen gas at an initial temperature of 20 ℃. If the final volume of the gas is 8 L at a final temperature of 50 ℃, then what was the initial volume of the gas according to Charles’s law?
Solution
Given data:
- Initial temperature of the gas, T1 = 20 ℃ = 293 K
- Final volume of the gas, V2 = 8 L
- Final temperature of the gas, T2 = 50 ℃ = 323 K
- Initial volume of the gas, V1 = ?
Applying the formula:
- V1/T1 = V2/T2
- V1 = (V2 × T1) ÷ T2
- V1 = (8 × 293) ÷ 323
- V1 = 2344 ÷ 323
- V1 = 7.25 L
Therefore, the initial volume of the gas is 7.25 L.
Problem #4
One box containing 4 L of argon gas is heated at an initial temperature. If the final temperature of the gas is 180 ℃ and the final volume of the gas is 6 L, then calculate the initial temperature of the gas.
Solution
Given data:
- Initial volume of the gas, V1 = 4 L
- Final temperature of the gas, T2 = 180 ℃ = 453 K
- Final volume of the gas, V2 = 6 L
- Initial temperature of the gas, T1 = ?
Applying the formula:
- V1/T1 = V2/T2
- T1 = (V1 × T2) ÷ V2
- T1 = (4 × 453) ÷ 6
- T1 = 1812 ÷ 6
- T1 = 302 K = 29 ℃
Therefore, the initial temperature of the gas is 29 ℃.
📝 Your feedback matters. Visit our contact page.
Related
More topics
- Boyle’s law
- Charles’s law
- Gay-Lussac’s law
- Avogadro’s law
- Ideal gas law
- Dalton’s law
- Henry’s law
- Combined gas law
- Graham’s law
External links
- Charles’s law – Wikipedia
- Charles’s law | Definition & Facts – Britannica
- 14.4: Charles’s Law – Chemistry LibreTexts
- Charles’s Law — Overview & Formula – Expii
- Charles’ Law | Formula, Units & Application – Study.com
- Charles’s Law – The University of Texas at Austin
- Charles’ Law Calculator – Omni Calculator
- Charles’s Law Definition in Chemistry – ThoughtCo
- Gas Laws – Florida State University
- Charles’ Law | Understanding Gas Laws – ChemTalk
- Charles’ Law (Jacques-Alexandre-César Charles) – Purdue University
- What is Charles’ law? – Scientific American
- 3 Ways to Demonstrate Charles’s Law – wikiHow
- Charles’s Law – Clippard
- Charles’ Law – Science Primer
- Animated Charles and Gay-Lussac’s Law – NASA (.gov)
- Gas Laws and Clinical Application – StatPearls – National Institutes of Health (.gov)
- Charles’s Law – HVAC School
- Charles Law – an overview – ScienceDirect
- Charles’ law – Oxford Reference
- Charles’ Law – Problems #1 – 10 – ChemTeam
- Charles’s Law – Definition, Formula, Examples – Science Notes and Projects
- Charles Law – Kent’s Chemistry
Deep
Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.