Dalton’s law

The information on this page is ✔ fact-checked.

Dalton’s law, also known as Dalton’s law of partial pressures, states that in a mixture of non-reacting gases, the total pressure exerted is equal to the sum of the partial pressures of individual gases. This law is based on the concept that each gas in a mixture behaves independently of the others, exerting its own pressure as if it were the only gas present in the container. In mathematical terms, if we have a mixture of gases A, B, and C, the total pressure (P_total) is equal to the sum of the partial pressures of each gas: P_total = P_A + P_B + P_C.

Dalton’s law is widely used in various fields, including the study of atmospheric gases, scuba diving, and industrial processes. For example, in scuba diving, this law is crucial for understanding how the pressure of different gases in a breathing mixture changes with depth. Similarly, in industrial processes such as gas storage and transportation, Dalton’s law helps engineers and scientists predict and control the behavior of gas mixtures under different conditions. This principle highlights its valuable insights into the behavior of gas mixtures, which have practical implications across a range of disciplines.

Formula

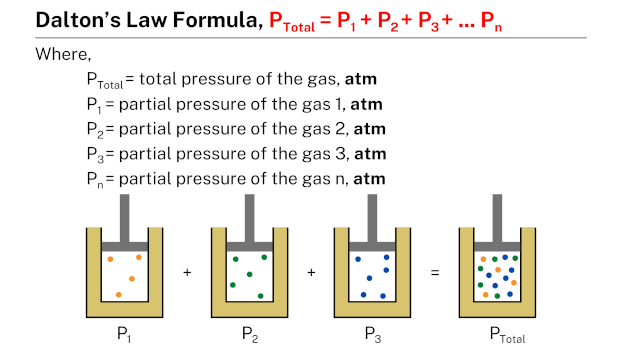
Dalton’s law formula, expressed as P_total = P₁ + P₂ + P₃ + … + P_n, states that the total pressure of a mixture of gases is equal to the sum of the partial pressures of the individual gases in the mixture. In this formula, P_total represents the total pressure of the gas mixture, while P₁, P₂, P₃, and so on, represent the partial pressures of each individual gas in the mixture.

Practice problems

Problem #1

A cylinder is filled with a mixture of radon, xenon, and helium gases. The mixture exerts a total pressure of 12 atm on the cylinder wall. The partial pressures of radon and xenon are 2 atm and 3 atm, respectively. Calculate the partial pressure of helium.

Solution

Given data:

• Total pressure of the gas, P_total = 12 atm
• Partial pressure of the radon gas, P₁ = 2 atm
• Partial pressure of the xenon gas, P₂ = 3 atm
• Partial pressure of the helium gas, P₃ = ?

Applying the formula:

• P_total = P₁ + P₂ + P₃ + … P_n
• P_total = P₁ +P₂ + P₃ (Because, a mixture is made up of three gases)
• 12 = 2 + 3 + P₃
• P₃ = 12 – 5
• P₃ = 7 atm

Therefore, the partial pressure of the helium gas is 7 atm.

Problem #2

In a solid container, there is a mixture of four gases with partial pressures of 4 atm, 3 atm, 5 atm, and 8 atm, respectively. Calculate the total pressure of the gas mixture.

Solution

Given data:

• Partial pressure of the gas 1, P₁ = 4 atm
• Partial pressure of the gas 2, P₂ = 3 atm
• Partial pressure of the gas 3, P₃ = 5 atm
• Partial pressure of the gas 4, P₄ = 8 atm
• Total pressure of the gas, P_total = ?

Applying the formula:

• P_total = P₁ + P₂ + P₃ + … P_n
• P_total = P₁ +P₂ + P₃ + P₄ (Because, a mixture is made up of four gases)
• P_total = 4 + 3 + 5 + 8
• P_total = 20 atm

Therefore, the total pressure of the gas is 20 atm.

Problem #3

A container is filled with a mixture of neon and krypton gases. If the total pressure of the mixture is 9 atm and the partial pressure of neon gas is 6 atm, calculate the partial pressure of krypton gas.

Solution

Given data:

• Total pressure of the gas, P_total = 9 atm
• Partial pressure of the neon gas, P₁ = 6 atm
• Partial pressure of the krypton gas, P₂ = ?

Applying the formula:

• P_total = P₁ + P₂ + P₃ + … P_n
• P_total = P₁ +P₂ (Because, a mixture is made up of two gases)
• 9 = 6 + P₂
• P₂ = 9 – 6
• P₂ = 3 atm

Therefore, the partial pressure of the krypton gas is 3 atm.

Problem #4

A container is filled with five gases that exert a total pressure of 24 atm on the container’s walls. The partial pressures of four of the gases are 2 atm, 5 atm, 6 atm, and 8 atm, respectively. What is the partial pressure of the fifth gas?

Solution

Given data:

• Total pressure of the gas, P_total = 24 atm
• Partial pressure of the gas 1, P₁ = 2 atm
• Partial pressure of the gas 2, P₂ = 5 atm
• Partial pressure of the gas 3, P₃ = 6 atm
• Partial pressure of the gas 4, P₄ = 8 atm
• Partial pressure of the gas 5, P₅ = ?

Applying the formula:

• P_total = P₁ + P₂ + P₃ + … P_n
• 24 = 2 +5 + 6 + 8 + P₅ (Because, a mixture is made up of five gases)
• 24 = 21 + P₅
• P₅ = 24 – 21 
• P₅ = 3 atm

Therefore, the partial pressure of the fifth gas is 3 atm.

📝 Your feedback matters. Visit our contact page.

Related

• Gas laws

More topics

• Boyle’s law
• Charles’s law
• Gay-Lussac’s law
• Avogadro’s law
• Ideal gas law
• Dalton’s law
• Henry’s law
• Combined gas law
• Graham’s law

External links

• Dalton’s law – Wikipedia
• Dalton’s Law (Law of Partial Pressures) – Chemistry LibreTexts
• Dalton’s law of partial pressure (article) – Khan Academy
• Dalton’s Law of Partial Pressure – an overview – ScienceDirect
• Ideal Gas Behavior: Dalton’s Law – Texas Gateway
• Dalton’s law | Definition & Facts – Britannica
• Dalton’s Law – The University of Texas at Austin
• Dalton’s Law of Partial Pressure | Formula & Examples – Study.com
• Dalton’s Law of Partial Pressures (John Dalton) – Purdue University
• Dalton’s law – Craft Beer & Brewing
• Daltons Law Relating Partial Pressure To Composition – Jack Westin
• Dalton’s Law of Partial Pressures — Overview & Calculation – Expii
• Dalton’s Law of Partial Pressures – CK-12
• Gas Law – Dalton’s Law and other partial pressure problems – ChemTeam
• How to Calculate Partial Pressures Using Dalton’s Law – Dummies
• What Is Dalton’s Law of Partial Pressures? – ThoughtCo