Germanium orbital diagram

The information on this page is ✔ fact-checked.

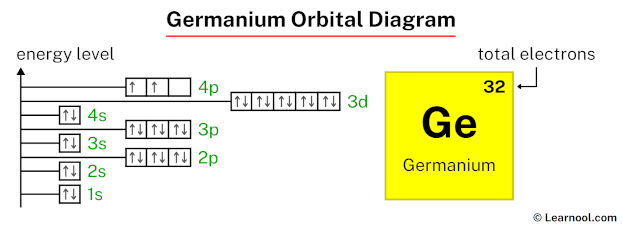
In the germanium orbital diagram, the 1s subshell accommodates two electrons, the 2s subshell holds another pair, the 2p subshell encompasses six electrons, the 3s subshell has two electrons, the 3p subshell accommodates six electrons, the 4s subshell holds two electrons, and the 3d subshell accommodates ten electrons. Lastly, the 4p subshell contains two electrons, totaling thirty-two electrons.

To illustrate the germanium orbital diagram, begin by determining the number of electrons from the periodic table. Take note of the electron configuration for reference and follow the three fundamental rules: the Aufbau principle, Pauli exclusion principle, and Hund’s rule. This systematic approach ensures an accurate representation of germanium’s orbital arrangement.

Steps

Find electrons

The atomic number of germanium represents the total number of electrons of germanium. Since the atomic number of germanium is 32, the total electrons of germanium are 32.

Write electron configuration

The electron configuration of germanium is 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p².

Learn how to find: Germanium electron configuration

Now in the next step, start drawing the orbital diagram for germanium.

Draw orbital diagram

Before drawing the orbital diagram, you should know the three general rules.

• Aufbau principle – electrons are first filled in lowest energy orbital and then in higher energy orbital
• Pauli exclusion principle – two electrons with the same spin can not occupy the same orbital
• Hund’s rule – each orbital should be first filled with one electron before being paired with a second electron

Also, you should know the number of orbitals in each subshell.

We can calculate the number of orbitals in each subshell using the formula: 2ℓ + 1

Where, ℓ = azimuthal quantum number of the subshell

For s subshell, ℓ = 0
For p subshell, ℓ = 1
For d subshell, ℓ = 2
For f subshell, ℓ = 3

So each s subshell has one orbital, each p subshell has three orbitals, each d subshell has five orbitals, and each f subshell has seven orbitals.

Now start to draw!

As mentioned above, the electron configuration of germanium is 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p². Hence, draw the blank orbital diagram of germanium up to 4p subshell as follows:

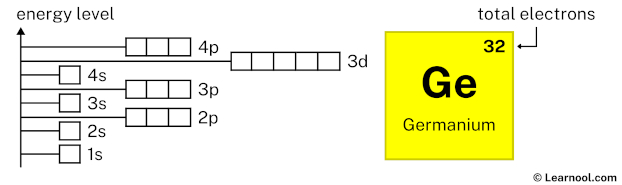
In the above orbital diagram, the box represents an orbital. Each orbital has a capacity of two electrons. And the arrows (↑↓) are drawn inside the box to represent electrons.

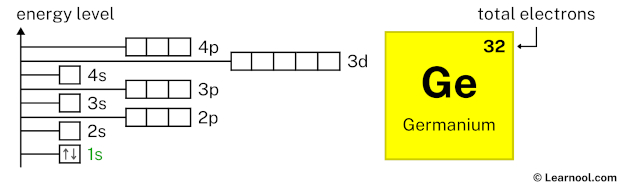
Now 1s² indicates that the 1s subshell has 2 electrons. So draw two arrows in the 1s box showing two electrons as follows:

2s² indicates that the 2s subshell has 2 electrons. So draw two arrows in the 2s box showing two electrons as follows:

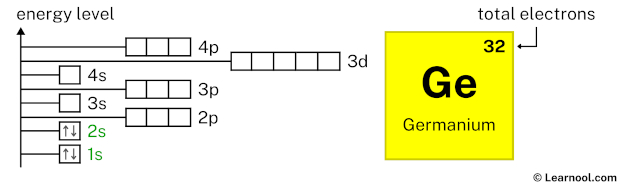
2p⁶ indicates that the 2p subshell has 6 electrons. So draw six arrows in the 2p box showing six electrons as follows:

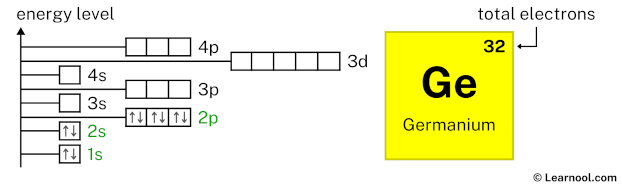
3s² indicates that the 3s subshell has 2 electrons. So draw two arrows in the 3s box showing two electrons as follows:

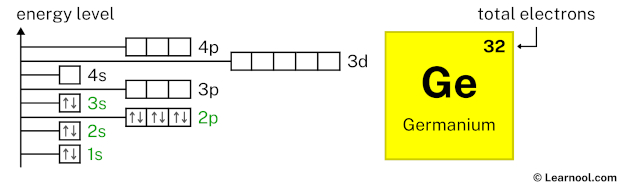
3p⁶ indicates that the 3p subshell has 6 electrons. So draw six arrows in the 3p box showing six electrons as follows:

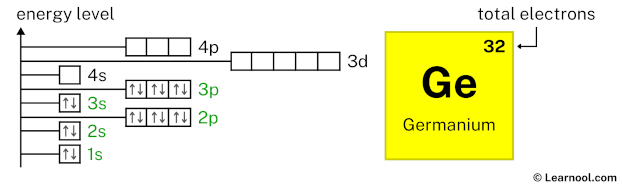
4s² indicates that the 4s subshell has 2 electrons. So draw two arrows in the 4s box showing two electrons as follows:

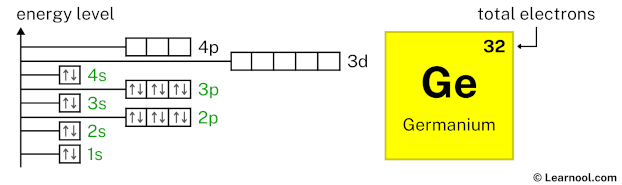
3d¹⁰ indicates that the 3d subshell has 10 electrons. So draw ten arrows in the 3d box showing ten electrons as follows:

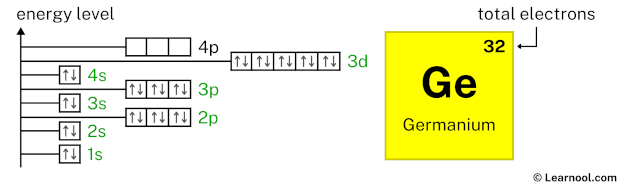
4p² indicates that the 4p subshell has 2 electrons. So draw two arrows in the 4p box showing two electrons as follows:

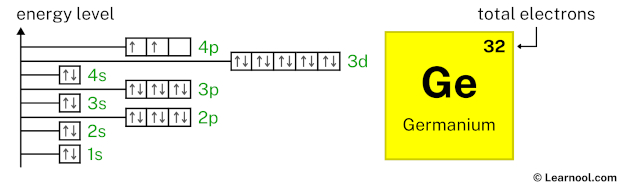
That’s it! This is the final orbital diagram of germanium as we have used all 32 electrons.

Next: Arsenic orbital diagram

📝 Your feedback matters. Visit our contact page.

Related

• Periodic table

More topics

• Germanium
• Germanium Bohr model
• Germanium electron configuration
• Germanium protons neutrons electrons
• Germanium valence electrons

External links

• https://www.numerade.com/questions/write-the-orbital-diagram-for-the-ground-state-of-the-germanium-atom-give-all-orbitals/
• https://www.chegg.com/homework-help/questions-and-answers/draw-orbital-diagram-germanium-ge-atom-germanium-paramagnetic-diamagnetic-q25484332