Henry’s law

The information on this page is ✔ fact-checked.

Henry’s law describes the relationship between the solubility of a gas in a liquid and the pressure of that gas above the liquid. It states that at a given temperature, the amount of gas dissolved in a liquid is directly proportional to the partial pressure of that gas. In simpler terms, this means that the higher the partial pressure of the gas above the liquid, the more gas molecules will dissolve into the liquid, and vice versa. Mathematically, this relationship can be expressed as C = k P, where C is the concentration of the gas in the liquid, k is Henry’s law constant for a specific gas and solvent at a particular temperature, and P is the partial pressure of the gas above the liquid.

This law has significant implications in various fields, notably in environmental science, chemistry, and engineering. In environmental science, Henry’s law helps in understanding the transfer of gases between the atmosphere and bodies of water, which is crucial for studying processes like gas exchange in aquatic ecosystems and the fate of pollutants. In chemistry and engineering, Henry’s law is applied in diverse areas such as gas absorption processes, carbonation of beverages, and the design of gas-liquid contactors in chemical reactors. Henry’s law allows scientists and engineers to predict and control the behavior of gas-liquid systems, making it an essential concept in many practical applications.

Equation

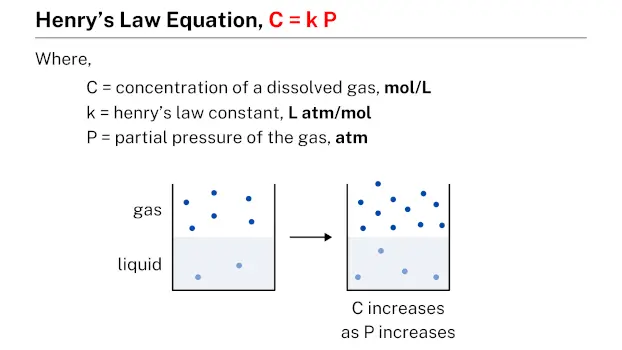
Henry’s law equation, represented by C = k P, describes the relationship between the concentration of a dissolved gas (C) in a given quantity of liquid and the partial pressure (P) of that gas. In this equation, k is a constant known as Henry’s law constant, which is specific to each gas-liquid system.

Practice problems

Problem #1

Calculate the concentration of oxygen gas dissolved in water, given that the partial pressure of the gas is 4 atm and the Henry’s law constant, k = 15 L atm/mol.

Solution

Given data:

• Concentration of a dissolved gas, C = ?
• Partial pressure of the gas, P = 4 atm
• Henry’s law constant, k = 15 L atm/mol

Applying the formula:

• C = k P
• C = 15 × 4
• C = 60 mol/L

Therefore, the concentration of a helium gas dissolved in water is 60 mol/L.

Problem #2

A liquid bottle contains a hydrogen gas concentration of 14 mol/L. Calculate the partial pressure of the gas, if the Henry’s law constant, k = 7 L atm/mol.

Solution

Given data:

• Concentration of a dissolved gas, C = 14 mol/L
• Partial pressure of the gas, P = ?
• Henry’s law constant, k = 7 L atm/mol

Applying the formula:

• C = k P
• 14 = 7 × P
• P = 2 atm

Therefore, the partial pressure of the gas is 2 atm.

Problem #3

If the partial pressure of argon gas in water is 6 atm and the Henry’s law constant is 25 L atm/mol, what is the concentration of argon gas dissolved in water?

Solution

Given data:

• Partial pressure of the gas, P = 6 atm
• Henry’s law constant, k = 25 L atm/mol
• Concentration of a dissolved gas, C = ?

Applying the formula:

• C = k P
• C = 25 × 6
• C = 150 mol/L

Therefore, the concentration of an argon gas dissolved in water is 150 mol/L.

Problem #4

Calculate the partial pressure of a hydrogen gas dissolved in water, given a concentration of 20 mol/L and the Henry’s law constant, k = 5 L atm/mol.

Solution

Given data:

• Partial pressure of the gas, P = ?
• Concentration of a dissolved gas, C = 20 mol/L
• Henry’s law constant, k = 5 L atm/mol

Applying the formula:

• C = k P
• 20 = 5 × P
• P = 4 atm

Therefore, the partial pressure of the gas is 4 atm.

📝 Your feedback matters. Visit our contact page.

Related

• Gas laws

More topics

• Boyle’s law
• Charles’s law
• Gay-Lussac’s law
• Avogadro’s law
• Ideal gas law
• Dalton’s law
• Henry’s law
• Combined gas law
• Graham’s law

External links

• Henry’s law – Wikipedia
• Henry’s Law – Chemistry LibreTexts
• Henry’s Law – StatPearls – National Institutes of Health (.gov)
• Henry’s law | Solubility, Gas-Liquid Equilibrium & Pressure – Britannica
• Henry’s Law – an overview – ScienceDirect
• Henry’s Law | Overview, Equation & Limitations – Study.com
• Henry’s Law – ChemTalk
• Henry’s Law of Solubility – CK-12
• Henry’s law – Craft Beer & Brewing
• Henry’s Law – Kent’s Chemistry
• Henry’s Law – Purdue University