Elastic energy refers to the potential energy stored in an object when it is deformed or stretched due to the application of a force. It is produced when an object undergoes elastic deformation, which means it can return to its original shape after the deforming force is removed. Objects possess elastic energy when they have the ability to store and release energy as a result of their elasticity. This energy is closely related to Hooke’s law, which states that the force needed to deform an object is directly proportional to the amount of deformation. When a force deforms an elastic object, such as compressing a spring or stretching a rubber band, elastic energy is stored within the object. This energy can be released and converted into other forms of energy when the object returns to its original shape. The ability of objects to store and release elastic energy is fundamental in various applications, from mechanical systems and structures to sports equipment and toys.
Examples
Resistance band

A resistance band is designed to provide resistance during exercises, and it demonstrates the principles of elastic energy. When a resistance band is stretched, the elastic material within the band undergoes deformation, storing elastic potential energy. This stored energy is released as the band is allowed to return to its original shape. The resistance band thus provides a form of resistance training, where the user works against the elastic force generated by the band. The controlled release of stored elastic potential energy contributes to muscle engagement and strength-building during various exercises.
Bow and arrow

Elastic energy is prominently demonstrated in a bow and arrow system. When an archer pulls back the bowstring, they are storing potential energy in the elastic material of the bowstring. The bowstring acts like a stretched spring, accumulating elastic potential energy. Upon release, the stored energy is rapidly transferred to the arrow, propelling it forward. The kinetic energy of the arrow in flight is a result of the release of the elastic potential energy stored in the bowstring. The bow and arrow exemplify the conversion of elastic potential energy into kinetic energy in projectile motion.
Rubber band

Stretching a rubber band with a hand exemplifies the elastic properties of rubber. As the rubber band is stretched, it undergoes deformation, storing elastic potential energy within its molecular structure. Releasing the tension allows the rubber band to quickly return to its original shape, and the stored potential energy is converted into kinetic energy. The rapid snapping or recoiling of the rubber band demonstrates the release of elastic potential energy, showcasing the material’s ability to stretch and return to its original form.
Stress ball

A stress ball, typically made of a squeezable and elastic material, demonstrates the storage and release of elastic energy. When the stress ball is squeezed, it deforms, and the material stores elastic potential energy. Releasing the squeeze allows the ball to return to its original shape, and the stored potential energy is converted into kinetic energy. The repetitive action of squeezing and releasing the stress ball provides a therapeutic and stress-relieving experience, illustrating the concept of elastic energy in a handheld device.
Pinball

In a pinball machine, elastic energy is showcased through the interactions of the spring-loaded plunger and the rebounding bumpers. When a player pulls and releases the plunger, they compress a spring. The compressed spring stores elastic potential energy. Upon release, the spring rapidly expands, converting the stored potential energy into kinetic energy that propels the pinball into play. As the pinball bounces off various obstacles and bumpers, the elastic collisions transfer energy back and forth between the ball and the machine’s components. The dynamic play of the pinball machine highlights the continuous conversion between elastic potential energy and kinetic energy.
Metal spring

When a metal spring is compressed or squished between fingers or hands, elastic energy is stored in the spring. As the spring is compressed, its coils come closer together, storing potential energy in the form of elastic deformation. Upon release, the spring rapidly expands back to its original shape, converting the stored elastic potential energy into kinetic energy. The action of squeezing and releasing the metal spring provides a tactile and audible example of the conversion between elastic potential energy and mechanical motion.
Bungee cord

A bungee cord is a specialized elastic cord used for activities like bungee jumping. When a person jumps off a platform with a bungee cord attached, the cord stretches and absorbs the gravitational potential energy of the jumper. The bungee cord stores this potential energy in the form of elastic potential energy as it elongates. The cord then recoils, releasing the stored energy and decelerating the jumper before reaching the lowest point of the jump. Bungee jumping highlights the controlled conversion of gravitational potential energy into elastic potential energy and back, providing a thrilling and dynamic experience.
Balloon

A balloon provides a simple yet illustrative example of elastic energy. When a balloon is inflated, the elastic material of the balloon stretches to accommodate the increasing volume of air inside. The stretched rubber stores elastic potential energy. When the balloon is released, the stored potential energy is rapidly converted into kinetic energy, causing the balloon to fly around the room. The elastic nature of the balloon allows for the repeated cycle of inflation, storage of potential energy, and release. Balloons serve as playful examples of how elastic energy can be harnessed for entertaining and dynamic effects.
Dart gun

A dart gun generates sound energy during its operation. When a dart is propelled through the barrel of the gun by a forceful exhale or a compressed air mechanism, the rapid movement of the dart creates air disturbances. These disturbances result in the production of sound waves that travel through the air. The sound generated can vary based on factors such as the force of the exhale, the design of the dart gun, and the type of dart used. The sharp, hissing sound produced during the dart’s flight exemplifies the conversion of mechanical energy into sound energy, enhancing the auditory experience of using a dart gun.
Ballpoint pen

A ballpoint pen utilizes elastic energy in its retractable mechanism. When the user clicks the pen to extend or retract the ballpoint, they engage a small spring-loaded mechanism inside the pen. The spring compresses when the pen is clicked, storing elastic potential energy. Upon releasing the clicker, the spring rapidly expands, pushing the ballpoint out or retracting it. The conversion between the compressed spring’s potential energy and the mechanical movement of the pen demonstrates the use of elastic energy in a convenient and functional writing instrument.
Formula
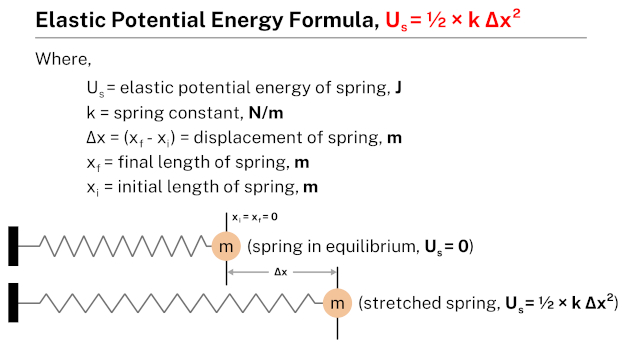
The elastic potential energy formula, expressed as Us = ½ × k Δx2, establishes a relationship between the elastic potential energy (Us) of a spring, the spring constant (k), and the square of the displacement (Δx). By utilizing this formula, one can calculate the amount of elastic potential energy stored in a spring, taking into account the spring constant and the square of the displacement. It’s worth noting that the displacement (Δx) is positive when the spring is stretched and negative when the spring is compressed.
Practice problems
Problem #1
Calculate the elastic potential energy of a spring when it is stretched from a length of 0.15 m to 0.30 m. Use a value of the spring constant, k = 150 N/m.
Solution
Given data:
- Elastic potential energy of a spring, Us = ?
- Initial length of a spring, xi = 0.15 m
- Finial length of a spring, xf = 0.30 m
- Therefore, the displacement of spring, Δx = xf – xi = 0.15 m
- Spring constant, k = 150 N/m
Applying the formula:
- Us = ½ × k Δx2
- Us = ½ × 150 × (0.15)2
- Us = ½ × 150 × 0.0225
- Us = 1.68 J
Therefore, the elastic potential energy of a spring is 1.68 J.
Problem #2
A spring initially measuring 5 m in length is compressed to a final length of 2 m. Determine the elastic potential energy of the spring. Use a value of the spring constant, k = 120 N/m.
Solution
Given data:
- Initial length of a spring, xi = 5 m
- Finial length of a spring, xf = 2 m
- Therefore, the displacement of spring, Δx = xf – xi = -3 m
- Elastic potential energy of a spring, Us = ?
- Spring constant, k = 120 N/m
Applying the formula:
- Us = ½ × k Δx2
- Us = ½ × 120 × (-3)2
- Us = ½ × 120 × 9
- Us = 540 J
Therefore, the elastic potential energy of a spring is 540 J.
Problem #3
Find the elastic potential energy stored in a spring that is stretched from its rest length of 0.25 m to 0.45 m. The spring has a spring constant of k = 180 N/m.
Solution
Given data:
- Elastic potential energy of a spring, Us = ?
- Initial length of a spring, xi = 0.25 m
- Finial length of a spring, xf = 0.45 m
- Therefore, the displacement of spring, Δx = xf – xi = 0.2 m
- Spring constant, k = 180 N/m
Applying the formula:
- Us = ½ × k Δx2
- Us = ½ × 180 × (0.2)2
- Us = 90 × 0.04
- Us = 3.6 J
Therefore, the elastic potential energy stored in a spring is 3.6 J.
Problem #4
A 0.85 m spring is fixed in the wall. Determine the elastic potential energy stored in the spring, when it is compressed to a length of 0.35 m. Use a spring constant value of k = 130 N/m.
Solution
Given data:
- Elastic potential energy of a spring, Us = ?
- Initial length of a spring, xi = 0.85 m
- Finial length of a spring, xf = 0.35 m
- Therefore, the displacement of spring, Δx = xf – xi = -0.5 m
- Spring constant, k = 130 N/m
Applying the formula:
- Us = ½ × k Δx2
- Us = ½ × 130 × (-0.5)2
- Us = ½ × 130 × 0.25
- Us = 16.25 J
Therefore, the elastic potential energy stored in a spring is 16.25 J.
Related
More topics
- Thermal energy
- Potential energy
- Kinetic energy
- Chemical energy
- Electrical energy
- Geothermal energy
- Radiant energy
- Sound energy
- Elastic energy
- Gravitational energy
- Mechanical energy
- Electric potential energy
- Rotational energy
- Photon energy
External links
- https://www.khanacademy.org/science/physics/work-and-energy/hookes-law/a/what-is-elastic-potential-energy
- https://www.solarschools.net/knowledge-bank/energy/types/elastic
- https://www.studysmarter.us/explanations/physics/energy-physics/elastic-potential-energy/
- https://lambdageeks.com/elastic-potential-energy-examples/
- https://study.com/learn/lesson/elastic-potential-energy-formula-equation.html
Deep
Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.
