The information on this page is ✔ fact-checked.
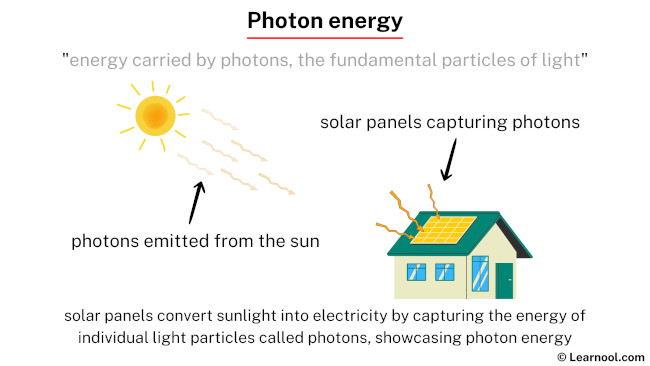
Photon energy refers to the energy carried by photons, which are fundamental particles of light. In the quantum realm, photons exhibit both particle and wave-like properties. Radio waves and microwaves; infrared and ultraviolet light; X-rays and gamma rays – all of these are forms of light, composed of photons. In various everyday scenarios, objects emit or exhibit photon energy. For instance, the glow of a light bulb or the warmth from the Sun can be attributed to the emission of photons, showcasing the practical significance of photon energy in our surroundings.
Equation
The photon energy equation states that the energy of a photon is directly proportional to its frequency, expressed as E = hf, where ‘E’ is the energy, ‘h’ is Planck’s constant, and ‘f’ is the frequency. This equation can also be expressed in terms of wavelength as E = hc/λ, highlighting a reciprocal relationship between photon energy and wavelength, where ‘c’ is the speed of light, and ‘λ’ is the wavelength.
Practice problems
Problem #1
Calculate the energy of a photon with a frequency of 4.54 × 106 Hz. Take the value of Planck’s constant as h = 6.626 × 10-34 J s.
Solution
Given data:
- Energy of a photon, E = ?
- Frequency of a photon, f = 4.54 × 106 Hz
- Planck’s constant, h = 6.626 × 10-34 J s
Applying the formula:
- E = hf
- E = 6.626 × 10-34 × 4.54 × 106
- E = 30.08 × 10-28 J
Therefore, the energy of a photon is 30.08 × 10-28 J.
Problem #2
A photon has a wavelength of 450 nm. Determine the energy of the photon. Take the values of Planck’s constant as h = 6.626 × 10-34 J s and the speed of light as c = 3 × 108 m/s.
Solution
Given data:
- Wavelength of a photon, λ = 450 nm = 450 × 10-9 m
- Energy of a photon, E = ?
- Planck’s constant, h = 6.626 × 10-34 J s
- Speed of light, c = 3 × 108 m/s
Applying the formula:
- E = hc/λ
- E = (6.626 × 10-34 × 3 × 108) ÷ (450 × 10-9)
- E = 0.0441 × 10-17 J
Therefore, the energy of a photon is 0.0441 × 10-17 J.
Problem #3
Calculate the energy of a photon with a frequency of 2.35 × 109 Hz. Take the value of Planck’s constant as h = 6.626 × 10-34 J s.
Solution
Given data:
- Energy of a photon, E = ?
- Frequency of a photon, f = 2.35 × 109 Hz
- Planck’s constant, h = 6.626 × 10-34 J s
Applying the formula:
- E = hf
- E = 6.626 × 10-34 × 2.35 × 109
- E = 15.57 × 10-25 J
Therefore, the energy of a photon is 15.57 × 10-25 J.
Problem #4
Determine the energy of a photon with a wavelength of 750 nm. Take the values of Planck’s constant as h = 6.626 × 10-34 J s and the speed of light as c = 3 × 108 m/s.
Solution
Given data:
- Energy of a photon, E = ?
- Wavelength of a photon, λ = 750 nm = 750 × 10-9 m
- Planck’s constant, h = 6.626 × 10-34 J s
- Speed of light, c = 3 × 108 m/s
Applying the formula:
- E = hc/λ
- E = (6.626 × 10-34 × 3 × 108) ÷ (750 × 10-9)
- E = 0.0265 × 10-17 J
Therefore, the energy of a photon is 0.0265 × 10-17 J.
📝 Your feedback matters. Visit our contact page.
Related
More topics
- Thermal energy
- Potential energy
- Kinetic energy
- Chemical energy
- Electrical energy
- Geothermal energy
- Radiant energy
- Sound energy
- Elastic energy
- Gravitational energy
- Mechanical energy
- Electric potential energy
- Rotational energy
- Photon energy
Deep
Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.