Electric potential energy is the stored energy of a charged particle within an electric field, determined by its position. It’s measured in joules and varies based on the arrangement of charges within a system, including both the charge’s own configuration and its position relative to other charged objects.
The term “electric potential energy” is specifically used in systems with changing electric fields, while “electrostatic potential energy” is designated for systems with constant fields. For instance, in a system of charged points, it represents the work needed to bring them together from infinite distance, overcoming their natural repulsion. Similarly, the electric potential energy of a specific charge or charges is the total work done by an external agent, such as applying force, moving them from infinity to their current configuration without acceleration.
Example
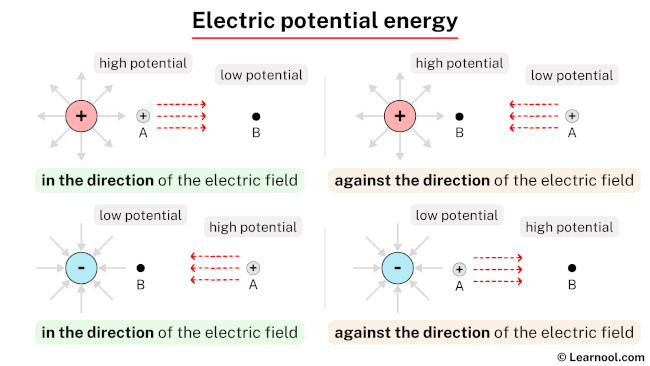
Charged particle behavior
When a charged particle moves in the direction of an electric field, its electric potential energy decreases, and this energy is typically converted into kinetic energy. This movement is analogous to an object moving downhill due to gravity, where its potential energy is converted into kinetic energy. The particle accelerates in the direction of the electric field, gaining speed and kinetic energy as it moves.
Conversely, when a charged particle moves against the direction of an electric field, its electric potential energy increases. In this scenario, external work must be done on the particle to move it against the field. This is akin to lifting an object against gravity, where energy is inputted to increase its potential energy. The particle loses kinetic energy and slows down as it moves against the field.
Formula
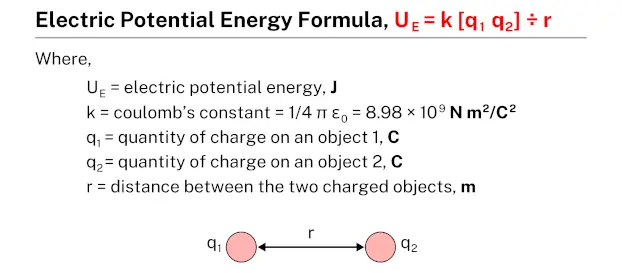
The electric potential energy formula, denoted as UE = k [q1 q2] ÷ r, establishes a relationship between the electric potential energy (UE) of a system, the Coulomb’s constant (k), the quantities of charges (q1 and q2), and the separation distance (r). This formula allows for the calculation of the electric potential energy based on the given values of charge quantities and their separation distance.
Practice problems
Problem #1
Calculate the electric potential energy of a system consisting of two balls, labeled 1 and 2, with charges of 15 µC and 35 µC respectively. The balls are separated by a distance of 2 m. Use a value of Coulomb’s constant, k = 8.98 × 109 N m2/C2.
Solution
Given data:
- Electric potential energy of the system, UE = ?
- Quantity of charge on ball 1, q1 = 15 µC = 15 × 10-6 C
- Quantity of charge on ball 2, q2 = 35 µC = 35 × 10-6 C
- Distance between the two charged balls, r = 2 m
- Coulomb’s constant, k = 8.98 × 109 N m2/C2
Applying the formula:
- UE = k [q1 q2] ÷ r
- UE = [(8.98 × 109) × (15 × 10-6) × (35 × 10-6)] ÷ 2
- UE = [8.98 × 15 × 35 × 10-3] ÷ 2
- UE = 4.7145 ÷ 2
- UE = 2.35 N
Therefore, the electric potential energy of the system is 2.35 N.
Problem #2
Two spheres, labeled 1 and 2, have charges q1 = 12 µC and q2 = 24 µC respectively. They are separated by a distance of 1 m. Find the electric potential energy of the system using a value of Coulomb’s constant, k = 8.98 × 109 N m2/C2.
Solution
Given data:
- Quantity of charge on sphere 1, q1 = 12 µC = 12 × 10-6 C
- Quantity of charge on sphere 2, q2 = 24 µC = 24 × 10-6 C
- Distance between the two charged spheres, r = 1 m
- Electric potential energy of the system, UE = ?
- Coulomb’s constant, k = 8.98 × 109 N m2/C2
Applying the formula:
- UE = k [q1 q2] ÷ r
- UE = [(8.98 × 109) × (12 × 10-6) × (24 × 10-6)] ÷ 1
- UE = [8.98 × 12 × 24 × 10-3] ÷ 1
- UE = 2.58 N
Therefore, the electric potential energy of the system is 2.58 N.
Problem #3
Determine the electric potential energy of a system in which two particles, A and B, have charges of 14 µC and 18 µC respectively. The particles are separated by a distance of 3 m. Use a value of Coulomb’s constant, k = 8.98 × 109 N m2/C2.
Solution
Given data:
- Electric potential energy of the system, UE = ?
- Quantity of charge on particle A, q1 = 14 µC = 14 × 10-6 C
- Quantity of charge on particle B, q2 = 18 µC = 18 × 10-6 C
- Distance between the two charged particles, r = 3 m
- Coulomb’s constant, k = 8.98 × 109 N m2/C2
Applying the formula:
- UE = k [q1 q2] ÷ r
- UE = [(8.98 × 109) × (14 × 10-6) × (18 × 10-6)] ÷ 3
- UE = [8.98 × 14 × 18 × 10-3] ÷ 3
- UE = 2.2629 ÷ 3
- UE = 0.75 N
Therefore, the electric potential energy of the system is 0.75 N.
Problem #4
Calculate the electric potential energy of a system in which two masses, labeled m1 and m2, have charges of 13 µC and 16 µC respectively. The masses are separated by a distance of 1.5 m. Use a value of Coulomb’s constant, k = 8.98 × 109 N m2/C2.
Solution
Given data:
- Electric potential energy of the system, UE = ?
- Quantity of charge on mass m1, q1 = 13 µC = 13 × 10-6 C
- Quantity of charge on mass m2, q2 = 16 µC = 16 × 10-6 C
- Distance between the two charged masses, r = 1.5 m
- Coulomb’s constant, k = 8.98 × 109 N m2/C2
Applying the formula:
- UE = k [q1 q2] ÷ r
- UE = [(8.98 × 109) × (13 × 10-6) × (16 × 10-6)] ÷ 1.5
- UE = [8.98 × 13 × 16 × 10-3] ÷ 1.5
- UE = 1.8678 ÷ 1.5
- UE = 1.24 N
Therefore, the electric potential energy of the system is 1.24 N.
Related
More topics
- Thermal energy
- Potential energy
- Kinetic energy
- Chemical energy
- Electrical energy
- Geothermal energy
- Radiant energy
- Sound energy
- Elastic energy
- Gravitational energy
- Mechanical energy
- Electric potential energy
- Rotational energy
- Photon energy
Deep
Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.
