Mechanical energy refers to the sum of potential energy and kinetic energy possessed by an object or a system. Potential energy is associated with the position or configuration of an object, while kinetic energy is related to its motion. Objects possess mechanical energy when they have the ability to perform work or cause a change in their surroundings. For example, a swinging pendulum possesses mechanical energy as it moves back and forth, with potential energy at the highest points of its swing and kinetic energy at the lowest point. Similarly, a compressed spring or a stretched rubber band has mechanical energy due to its potential to return to its original shape and release stored energy.
Examples
Hammer

Hammering a nail into a wall is a mechanical energy process that involves both kinetic and potential energy. As the hammer swings downward, it gains kinetic energy. Upon impact with the nail, the potential energy stored in the raised hammer is transferred to the nail, driving it into the wall. The repetitive action of lifting and swinging the hammer, followed by the kinetic energy release during the striking motion, exemplifies the mechanical energy involved in carpentry and construction tasks.
Dart gun

A dart gun operates through the conversion of mechanical energy. When the gun is loaded and the dart is placed in position, potential energy is stored in the compressed spring or elastic mechanism within the gun. Upon triggering, the potential energy is rapidly converted into kinetic energy as the spring releases, propelling the dart forward. The dart’s flight is a result of the mechanical energy transformation from stored potential energy to kinetic energy. Dart guns demonstrate the controlled use of mechanical energy for recreational activities.
Dumbbell

Lifting a dumbbell involves the application of mechanical energy. As a person raises the dumbbell against gravity, they perform work and impart kinetic energy to the dumbbell. The elevation of the dumbbell contributes to its potential energy. Throughout the lifting motion, the interplay between kinetic and potential energy showcases mechanical energy. The controlled execution of a dumbbell lift is a demonstration of how mechanical energy is harnessed in strength training exercises.
Bow and arrow

The interaction between a bow and arrow system involves mechanical energy transformations. When an archer pulls back the bowstring, they input mechanical work, storing potential energy in the elastic material of the bow. Upon release, the bowstring rapidly returns to its original position, converting potential energy into kinetic energy. Simultaneously, the arrow is propelled forward with kinetic energy. The coordinated movement of the bow and arrow system illustrates the transfer and transformation of mechanical energy, combining elastic potential energy and kinetic energy for accurate and effective arrow propulsion.
Bicycle

Riding a bicycle is a dynamic example of mechanical energy conversion. As a cyclist pedals, they input kinetic energy to the bicycle’s wheels, propelling it forward. The potential energy is also involved when the cyclist ascends a hill, storing energy that can be released as kinetic energy during the descent. The continuous interplay between the kinetic and potential energy of the moving bicycle demonstrates mechanical energy in action. The efficiency of a bicycle as a means of transportation relies on the effective conversion and utilization of mechanical energy.
Athlete

An athlete, engaged in various activities, exhibits mechanical energy through their movements. For instance, a runner demonstrates kinetic energy as they sprint, while a weightlifter showcases potential energy when lifting weights against gravity. The coordinated actions of muscles and joints contribute to the overall mechanical energy displayed by athletes during activities such as running, jumping, or throwing. Mechanical energy is fundamental to understanding and optimizing athletic performance across different sports.
Hydropower

Hydropower harnesses the mechanical energy of flowing water to generate electricity. As water flows or falls, it possesses kinetic energy. In a hydropower plant, this kinetic energy is captured by turbines connected to generators. The spinning turbines convert the kinetic energy of the moving water into mechanical energy, which is further transformed into electrical energy. The controlled release and utilization of the mechanical energy in flowing water highlight the efficiency of hydropower as a renewable energy source.
Wrecking ball

A wrecking ball is a striking example of mechanical energy used in demolition. As the wrecking ball swings, it gains kinetic energy due to its motion. The potential energy of the ball is heightened when it is lifted to a certain height before release. When the wrecking ball is released and swings into a structure, the stored potential energy is converted into kinetic energy, causing destructive impact. The controlled application of mechanical energy in a wrecking ball illustrates its efficiency in bringing down structures during demolition processes.
Bowling

A bowling ball possesses mechanical energy as a combination of its kinetic and potential energy. When a bowler rolls the ball down the lane, the ball’s motion is a manifestation of kinetic energy. Additionally, the elevation of the ball on the lane’s surface contributes to its potential energy. The total mechanical energy of the bowling ball is the sum of its kinetic and potential energy. The smooth interplay between these two forms of energy is crucial for achieving an effective and accurate roll.
Windmill

A windmill converts the kinetic energy of the wind into mechanical energy. As the wind blows, it imparts kinetic energy to the blades of the windmill. The spinning motion of the blades is then transferred to a generator, converting the mechanical energy into electrical energy. Windmills, particularly in wind farms, illustrate the utilization of wind energy as a clean and renewable source of mechanical energy that can be harnessed for electricity generation. The efficient conversion of wind’s kinetic energy into electricity showcases the principles of mechanical energy transformation.
Car

A car is a complex system that involves various forms of mechanical energy. When a car is in motion, the rotational movement of its wheels represents kinetic energy. The engine of the car converts fuel into mechanical energy to drive the vehicle. Brakes, on the other hand, convert the kinetic energy of the moving car into thermal energy through friction, slowing down or stopping the car. The interplay between kinetic and potential energy, along with various mechanical components, showcases the diverse mechanical energy transformations in a car.
Cricket

When a cricket ball is bowled, it exhibits mechanical energy in the form of kinetic energy. The bowler imparts kinetic energy to the ball as it travels towards the batsman. The energy is further transferred during the impact between the ball and the bat, showcasing the dynamic interplay of kinetic energy in the sport of cricket. The kinetic energy of the ball influences its trajectory, speed, and the potential for scoring runs or dismissing batsmen.
Electric motor

An electric motor is a device that converts electrical energy into mechanical energy. Inside the motor, an electric current interacts with a magnetic field, resulting in the generation of rotational motion. This rotational motion represents kinetic energy produced by the motor. Electric motors are commonly used in various applications, from household appliances to industrial machinery, showcasing their versatility in converting electrical energy into useful mechanical work. The efficiency and precision of electric motors make them essential components in countless devices that rely on mechanical energy for operation.
Moon

The Moon possesses mechanical energy through its orbital motion around the Earth. As the Moon orbits, it exhibits kinetic energy derived from its movement in the gravitational field of the Earth. Additionally, the Moon’s position in its orbit influences its gravitational potential energy. The gravitational interactions between the Moon and Earth, combined with the Moon’s motion, represent a dynamic system where mechanical energy is conserved. The cyclical changes in kinetic and potential energy contribute to phenomena like tides on Earth.
Formula
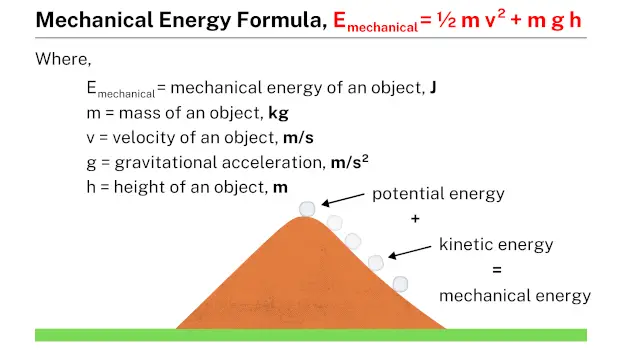
The mechanical energy formula, expressed as Emechanical = ½ m v2 + m g h, provides a way to calculate the total mechanical energy (Emechanical) of an object. It combines the contributions of kinetic energy (½ m v2) and potential energy (m g h). By utilizing this formula, one can determine the amount of mechanical energy possessed by an object based on its mass, velocity, gravitational acceleration, and height.
Practice problems
Problem #1
Calculate the mechanical energy of a 20 kg stone resting on the top of a hill at a height of 50 m. Take the value of gravitational acceleration as g = 9.81 m/s2.
Solution
Given data:
- Mechanical energy of a stone, Emechanical = ?
- Mass of a stone, m = 20 kg
- Height at which a stone is resting, h = 50 m
- Velocity of a stone, v = 0 m/s (Because, a stone is at rest)
- Gravitational acceleration, g = 9.81 m/s2
Applying the formula:
- Emechanical = ½ m v2 + m g h
- Emechanical = (0) + (20 × 9.81 × 50)
- Emechanical = 20 × 9.81 × 50
- Emechanical = 9,810 J
Therefore, the mechanical energy of a stone is 9,810 J.
Problem #2
A skydiver with a mass of 50 kg has a velocity of 20 m/s at a height of 100 m above the ground. Calculate the mechanical energy of the skydiver. Take the value of gravitational acceleration as g = 9.81 m/s2.
Solution
Given data:
- Mass of a skydiver, m = 50 kg
- Velocity of a skydiver, v = 20 m/s
- Height of a skydiver above the ground, h = 100 m
- Mechanical energy of a skydiver, Emechanical = ?
- Gravitational acceleration, g = 9.81 m/s2
Applying the formula:
- Emechanical = ½ m v2 + m g h
- Emechanical = [(½ × 50 × 202) + (50 × 9.81 × 100)]
- Emechanical = 10,000 + 49,050
- Emechanical = 59,050 J
Therefore, the mechanical energy of a skydiver is 59,050 J.
Problem #3
A 10 kg ball is rolling down a hill with a velocity of 12 m/s at a height of 30 m above the ground. Determine the mechanical energy of the ball. Take the value of gravitational acceleration as g = 9.81 m/s2.
Solution
Given data:
- Mass of a ball, m = 10 kg
- Velocity of a ball, v = 12 m/s
- Height of a ball above the ground, h = 30 m
- Mechanical energy of a ball, Emechanical = ?
- Gravitational acceleration, g = 9.81 m/s2
Applying the formula:
- Emechanical = ½ m v2 + m g h
- Emechanical = [(½ × 10 × 122) + (10 × 9.81 × 30)]
- Emechanical = 720 + 2943
- Emechanical = 3,663 J
Therefore, the mechanical energy of a ball is 3,663 J.
Problem #4
A football player kicks a football to a height of 12 m above the ground. If the mass of the football is 450 g and the velocity of the football is 8 m/s, calculate the mechanical energy of the football. Take the value of gravitational acceleration as g = 9.81 m/s2.
Solution
Given data:
- Height of a football above the ground, h = 12 m
- Mass of a football, m = 450 g = 0.45 kg
- Velocity of a football, v = 8 m/s
- Mechanical energy of a football, Emechanical = ?
- Gravitational acceleration, g = 9.81 m/s2
Applying the formula:
- Emechanical = ½ m v2 + m g h
- Emechanical = [(½ × 0.45 × 82) + (0.45 × 9.81 × 12)]
- Emechanical = 14.4 + 52.974
- Emechanical = 67.37 J
Therefore, the mechanical energy of a football is 67.37 J.
Related
More topics
- Thermal energy
- Potential energy
- Kinetic energy
- Chemical energy
- Electrical energy
- Geothermal energy
- Radiant energy
- Sound energy
- Elastic energy
- Gravitational energy
- Mechanical energy
- Electric potential energy
- Rotational energy
- Photon energy
External links
- https://justenergy.com/blog/mechanical-energy-beginners-guide/
- https://www.physicsclassroom.com/class/energy/Lesson-1/Mechanical-Energy
- https://examples.yourdictionary.com/examples-of-mechanical-energy-at-home-and-in-daily-life.html
- https://study.com/academy/lesson/what-are-the-types-of-energy.html
- https://www.britannica.com/science/mechanical-energy
- https://en.wikipedia.org/wiki/Mechanical_energy
Deep
Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.
