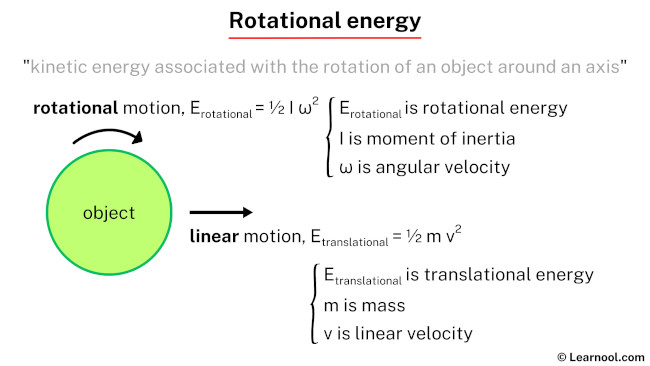
Rotational energy

by

The information on this page is ✔ fact-checked.

Rotational energy, also known as angular kinetic energy, is kinetic energy associated with the rotation of an object around an axis. When an object, such as a spinning wheel or a rotating top, undergoes rotational motion, it possesses rotational energy. This energy is dependent on both the mass distribution of the object and its angular velocity. In simpler terms, the faster an object rotates or the greater the distribution of mass away from the axis of rotation, the greater its rotational energy.

Formula

Rotational kinetic energy formula
Rotational kinetic energy formula | Image: Learnool

The rotational kinetic energy formula, represented as Erotational = ½ I ω2, describes the rotational energy of an object. In this equation, ‘I’ denotes the moment of inertia, indicating the object’s resistance to changes in rotation, while ‘ω’ represents the angular velocity, reflecting the speed of rotation. This concise formula illustrates the relationship between the distribution of mass (moment of inertia) and the rate of rotation (angular velocity), providing a quantitative measure of the rotational energy within the system.

When objects undergo linear motion, they carry translational energy – a reflection of their kinetic energy associated with straight-line movement. This energy is calculated using the formula Etranslational = ½ m v2, where ‘m’ represents the mass of the object, and ‘v’ stands for its linear velocity. Essentially, the mass and speed of an object significantly contribute to defining its translational energy, providing a numerical representation of its motion through space.

Practice problems

Problem #1

Calculate the rotational kinetic energy of an object with a moment of inertia of 2 kg m2, rotating with an angular velocity of 4 rad/s.

Solution

Given data:

  • Rotational kinetic energy of an object, KErotational = ?
  • Moment of inertia of an object, I = 2 kg m2
  • Angular velocity of an object, ω = 4 rad/s

Applying the formula:

  • KEroatational = ½ I ω2
  • KEroatational = ½ × 2 × (4)2
  • KEroatational = 16 J

Therefore, the rotational kinetic energy of an object is 16 J.

Problem #2

A football is rotating with an angular velocity of 15 rad/s and has a moment of inertia of 1 kg m2. Calculate the rotational kinetic energy of the football.

Solution

Given data:

  • Angular velocity of a football, ω = 15 rad/s
  • Moment of inertia of a football, I = 1 kg m2
  • Rotational kinetic energy of a football, KErotational = ?

Applying the formula:

  • KEroatational = ½ I ω2
  • KEroatational = ½ × 15 × (1)2
  • KEroatational = 7.5 J

Therefore, the rotational kinetic energy of a football is 7.5 J.

Problem #3

What is the rotational kinetic energy of a sharpening wheel with a moment of inertia of 30 kg m2, rotating with an angular velocity of 6 rad/s?

Solution

Given data:

  • Rotational kinetic energy of a sharpening wheel, KErotational = ?
  • Moment of inertia of a sharpening wheel, I = 30 kg m2
  • Angular velocity of a sharpening wheel, ω = 6 rad/s

Applying the formula:

  • KEroatational = ½ I ω2
  • KEroatational = ½ × 30 × (6)2
  • KEroatational = 15 × 36
  • KEroatational = 540 J

Therefore, the rotational kinetic energy of a sharpening wheel is 540 J.

Problem #4

A disc placed in a DVD player rotates with an angular velocity of 8 rad/s. If the disc has a moment of inertia of 7 kg m2, then calculate the rotational kinetic energy of the disc.

Solution

Given data:

  • Angular velocity of a disc, ω = 8 rad/s
  • Moment of inertia of a disc, I = 7 kg m2
  • Rotational kinetic energy of a disc, KErotational = ?

Applying the formula:

  • KEroatational = ½ I ω2
  • KEroatational = ½ × 7 × (8)2
  • KEroatational = ½ × 7 ×64
  • KErotational = 7 × 32
  • KEroatational = 224 J

Therefore, the rotational kinetic energy of a disc is 224 J.

Related

More topics

Deep

Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.

Leave a Comment